题目内容
判断函数f（x）=lnx+x2-3的零点个数是 ．
考点：根的存在性及根的个数判断
专题：计算题,函数的性质及应用
分析：判断根的个数要用函数的单调性与根的存在性定理．
解答：
解：∵f（x）=lnx+x2-3的定义域为（0，+∞），
又∵f′（x）=
+2x=
＞0，
则f（x）=lnx+x2-3在定义域（0，+∞）内至多有一个零点，
又∵f（1）=-2＜0，f（e）=1+e2-3＞0，
则f（x）=lnx+x2-3在定义域（0，+∞）内有且只有一个零点．
故答案为1．
又∵f′（x）=
| 1 |
| x |
| 1+2x2 |
| x |
则f（x）=lnx+x2-3在定义域（0，+∞）内至多有一个零点，
又∵f（1）=-2＜0，f（e）=1+e2-3＞0，
则f（x）=lnx+x2-3在定义域（0，+∞）内有且只有一个零点．
故答案为1．
点评：本题考查了函数零点个数的判断，属于中档题．
练习册系列答案
相关题目
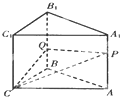如图，在三棱柱的侧棱A1A和B1B上各有一动点P，Q，且满足A1P=BQ，过P、Q、C三点的截面把棱柱分成两部分，则其上下体积之比为