题目内容
15.(1)等差数列{an}中,a5=11,a8=5,求该数列的通项公式;(2)已知等差数列{an}中,a1=2,a2和a3是两个连续正整数的平方,求该数列的通项公式.
分析 (1)利用等差数列通项公式列出方程组求出首项和公差,由此能求出该数列的通项公式.
(2)设a2=n2,${a}_{3}=(n+1)^{2}$,n∈Z+,由等差数列的性质求出公差,由此能求出该数列的通项公式.
解答 解:(1)∵等差数列{an}中,a5=11,a8=5,
∴$\left\{\begin{array}{l}{{a}_{1}+4d=11}\\{{a}_{1}+7d=5}\end{array}\right.$,
a1=19,d=-2,
∴该数列的通项公式an=19+(n-1)×(-2)=21-2n.
(2)∵等差数列{an}中,a1=2,a2和a3是两个连续正整数的平方,
∴设a2=n2,${a}_{3}=(n+1)^{2}$,n∈Z+,
∴2n2=2+(n+1)2,
解得n=3,或n=-1(舍),
∴${a}_{2}={3}^{2}=9$,${a}_{4}={4}^{2}$=16,
∴d=9-2=7,
该数列的通项公式an=2+(n-1)×7=7n-5.
点评 本题考查等差数列的通项公式的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
6.若$\frac{5π}{2}$<α<3π,则$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cosα}}$等于( )
| A. | cos$\frac{α}{4}$ | B. | -cos$\frac{α}{4}$ | C. | sin$\frac{α}{4}$ | D. | -sin$\frac{α}{4}$ |
3.在区间[0,2]上任取两个实数a、b,则函数f(x)=x2+ax-$\frac{1}{4}$b2+1在区间(-1,1)没有零点的概率为( )
| A. | $\frac{π}{8}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{4-π}{8}$ | D. | $\frac{π}{4}$ |
10.在Rt△ABC中,∠A为直角,且AB=3,BC=5,若在三角形ABC内任取一点,则该点到三个定点A,B,C的距离不小于1的概率是( )
| A. | $\frac{π}{6}$ | B. | 1-$\frac{π}{6}$ | C. | $\frac{π}{12}$ | D. | 1-$\frac{π}{12}$ |
20.已知抛物线C:y2=2px(p>0),直线l与抛物线C交于A,B两点(不同于原点),以AB为直径的圆过坐标原点O,则关于直线l的判断正确的是( )
| A. | 过定点(4p,0) | B. | 过定点(2p,0) | C. | 过定点(p,0) | D. | 过抛物线焦点 |
7.已知函数f(x)=4sin(2x+$\frac{π}{6}$),x∈R,则下列命题正确的是( )
| A. | f(x)在区间[0,$\frac{π}{2}$]内是增函数 | |
| B. | 若?x1≠x2,f(x1)=f(x2)=0,则x1-x2必是π的整数倍 | |
| C. | f(x)的图象关于点(-$\frac{π}{12}$+$\frac{kπ}{2}$,0)(k∈Z)对称 | |
| D. | f(x)的图象关于直线x=$\frac{π}{12}$对称 |
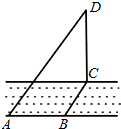 如图,在河的一侧有一塔CD=12m,河宽BC=3m,另一侧有点A,AB=4m,则点A与塔顶D的距离AD=13.
如图,在河的一侧有一塔CD=12m,河宽BC=3m,另一侧有点A,AB=4m,则点A与塔顶D的距离AD=13.