题目内容
17. 甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )| A. | $\overline{x_1}$>$\overline{x{\;}_2}$,$S_1^2$<$S_2^2$ | B. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$>$S_2^2$ | ||
| C. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$=$S_2^2$ | D. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$<$S_2^2$ |
分析 分别计算甲、乙运动员成绩的平均数与方差,进行比较即可.
解答 解:根据茎叶图中的数据,得;
甲运动员成绩的平均数是$\overline{{x}_{1}}$=$\frac{1}{6}$(8+13+15+15+17+22)=15,
方差是${{s}_{1}}^{2}$=$\frac{1}{6}$[(8-15)2+(13-15)2+2×(15-15)2+(17-15)2+(22-15)2]=$\frac{53}{3}$;
乙运动员成绩的平均数是$\overline{{x}_{2}}$=$\frac{1}{6}$(9+14+15+15+16+21)=15,
方差是${{s}_{2}}^{2}$=$\frac{1}{6}$[(9-15)2+(14-15)2+2×(15-15)2+(16-15)2+(21-15)2]=$\frac{37}{3}$;
∴$\overline{{x}_{1}}$=$\overline{{x}_{2}}$,${{s}_{1}}^{2}$>${{s}_{2}}^{2}$.
故选:B.
点评 本题考查了利用茎叶图中的数据求平均数与方差的问题,是基础题目.

练习册系列答案
相关题目
8.已知某几何体的三视图如上图所示,则该几何体的体积为( )
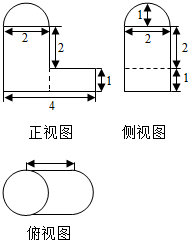

| A. | 3+$\frac{10}{3}$π | B. | 4+$\frac{11}{3}$π | C. | 3+$\frac{11}{3}$π | D. | 4+$\frac{8}{3}$π |
5.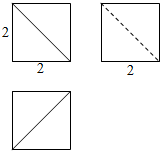 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{20}{3}$ | B. | 18 | C. | $24+2\sqrt{3}$ | D. | $18+2\sqrt{3}$ |
12.已知函数f(x)=(m+2)x2+mx+1为偶函数,则f(x)在区间(1,+∞)上是( )
| A. | 先增后减 | B. | 先减后增 | C. | 减函数 | D. | 增函数 |
9.“x2-1>0”是“x>1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
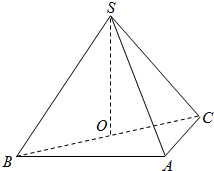 如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.