题目内容
已知数列{an}中,点(an,an+1)(n∈N*)在直线x-y+1=0上,且a2=2.
(Ⅰ)求证:数列{an}是等差数列,并求an;
(Ⅱ)设bn=3an,数列{bn}的前n项和为Sn,若对任意n∈N*,都有(n+1)(2Sn+3)≤λ•4n恒成立,求实数λ的取值范围.
(Ⅰ)求证:数列{an}是等差数列,并求an;
(Ⅱ)设bn=3an,数列{bn}的前n项和为Sn,若对任意n∈N*,都有(n+1)(2Sn+3)≤λ•4n恒成立,求实数λ的取值范围.
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)把点(an,an+1)代入直线x-y+1=0,整理后得到数列{an}是等差数列,结合a2=2求出首项,则等差数列的通项公式可求;
(Ⅱ)把an代入bn=3an,得到数列{bn}是等比数列,求出其钱n项和,代入(n+1)(2Sn+3)≤λ•4n后分离参数λ,构造数列cn=3(n+1)(
)n(n∈N*),求出数列{cn}的最大项后得答案.
(Ⅱ)把an代入bn=3an,得到数列{bn}是等比数列,求出其钱n项和,代入(n+1)(2Sn+3)≤λ•4n后分离参数λ,构造数列cn=3(n+1)(
| 3 |
| 4 |
解答:
解:(Ⅰ)由题意,点(an,an+1)(n∈N*)在直线x-y+1=0上,
∴an-an+1+1=0,
即an+1-an=1(n∈N*),
又a2=2,
∴a1=1.
因此,数列{an}是公差、首项均为1的等差数列,
通项公式为an=n(n∈N*);
(Ⅱ)由bn=3an及an=n(n∈N*),
得bn=3n(n∈N*),其前n项和Sn=
=
-
,
又对任意n∈N*,都有(n+1)(2Sn+3)≤λ•4n恒成立,
即(n+1)3n+1≤λ•4n,λ≥3(n+1)(
)n恒成立.
记cn=3(n+1)(
)n(n∈N*),
由
,
即
,得2≤n≤3,
∴{cn}的最大项为c2=c3=3×4×(
)3=
.
从而实数λ的取值范围为[
,+∞).
∴an-an+1+1=0,
即an+1-an=1(n∈N*),
又a2=2,
∴a1=1.
因此,数列{an}是公差、首项均为1的等差数列,
通项公式为an=n(n∈N*);
(Ⅱ)由bn=3an及an=n(n∈N*),
得bn=3n(n∈N*),其前n项和Sn=
| 3×(1-3n) |
| 1-3 |
| 3n+1 |
| 2 |
| 3 |
| 2 |
又对任意n∈N*,都有(n+1)(2Sn+3)≤λ•4n恒成立,
即(n+1)3n+1≤λ•4n,λ≥3(n+1)(
| 3 |
| 4 |
记cn=3(n+1)(
| 3 |
| 4 |
由
|
即
|
∴{cn}的最大项为c2=c3=3×4×(
| 3 |
| 4 |
| 81 |
| 16 |
从而实数λ的取值范围为[
| 81 |
| 16 |
点评:本题考查了数列的函数特性,考查了等差关系的确定,训练了分离变量法和函数构造法,求解数列{cn}的最大项是解答该题的关键,属难题.

练习册系列答案
相关题目
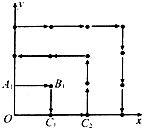 某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点Al(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么:
某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点Al(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么: