题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},}&{x≤1}\\{x+\frac{4}{x}-3,}&{x>1}\end{array}\right.$,则f(x)的值域是( )| A. | [1,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | [0,1)∪(1,+∞) |
分析 求出x≤1时二次函数的值域,再由基本不等式求出x>1时函数的值域,取并集得答案.
解答 解:由f(x)=$\left\{\begin{array}{l}{{x}^{2},}&{x≤1}\\{x+\frac{4}{x}-3,}&{x>1}\end{array}\right.$,知
当x≤1时,x2≥0;
当x>1时,x+$\frac{4}{x}$-3≥2$\sqrt{x•\frac{4}{x}}$-3=4-3=1,当且仅当x=$\frac{4}{x}$,即x=2时取“=”,
取并集得:f(x)的值域是[0,+∞).
故选:B.
点评 本题考查分段函数值域的求法,分段函数的值域分段求,然后取并集即可,是中档题.

练习册系列答案
相关题目
7.阅读程序框图,该算法的功能是输出( )
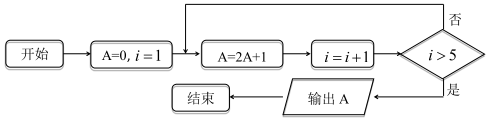

| A. | 数列{2n-1}的前 4项的和 | B. | 数列{2n-1}的第4项 | ||
| C. | 数列{2n}的前5项的和 | D. | 数列?{2n-1}的第5项 |
4.在平面直角坐标系中,已知点A,B分别为x轴、y轴上的点,且|AB|=1,若点P(1,$\frac{4}{3}})$),则$|{\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{OP}}$|的取值范围是( )
| A. | [5,6] | B. | [5,7] | C. | [4,6] | D. | [6,9] |
8.在平面直角坐标系xOy中,已知抛物线C:x2=4y,点P是C的准线l上的动点,过点P作C的两条切线,切点分别为A,B,则△AOB面积的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
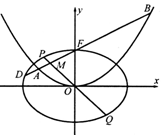 如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.
如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.