题目内容
设数列{an}满足an=3an-1+2(n≥2,n∈N*),且a1=2,bn=log3(an+1).
(1)证明:数列{an+1}为等比数列;
(2)求数列{anbn}的前n项和Sn.
(1)证明:数列{an+1}为等比数列;
(2)求数列{anbn}的前n项和Sn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)由数列{an}满足an=3an-1+2(n≥2,n∈N*),变形an+1=3(an-1+1),即可证明;
(2)利用“错位相减法”、等比数列的前n项和公式,即可得出.
(2)利用“错位相减法”、等比数列的前n项和公式,即可得出.
解答:
(1)证明:∵数列{an}满足an=3an-1+2(n≥2,n∈N*),
∴an+1=3(an-1+1),
又a1+1=3,
∴数列{an+1}为等比数列.
(2)由(1)知an+1=3n,∴an=3n-1,
∴bn=log3(an+1)=n.
∴anbn=n•(3n-1)=n•3n-n,
设Tn=1×3+2×32+3×33+…+n•3n,
∴3Tn=32+2×33+…+(n-1)×3n+n×3n+1,
∴-2Tn=3+32+33+…+3n-n×3n+1=
-n×3n+1=
-n×3n+1,
∴Tn=
+
×3n+1.
∴an+1=3(an-1+1),
又a1+1=3,
∴数列{an+1}为等比数列.
(2)由(1)知an+1=3n,∴an=3n-1,
∴bn=log3(an+1)=n.
∴anbn=n•(3n-1)=n•3n-n,
设Tn=1×3+2×32+3×33+…+n•3n,
∴3Tn=32+2×33+…+(n-1)×3n+n×3n+1,
∴-2Tn=3+32+33+…+3n-n×3n+1=
| 3(3n-1) |
| 3-1 |
| 3n+1-3 |
| 2 |
∴Tn=
| 3-3n |
| 4 |
| n |
| 2 |
点评:本题考查了“错位相减法”、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知三个向量
,
,
两两所夹的角都为120°,且|
|=1,|
|=2,|
|=3,则向量
+
与向量
的夹角θ的值为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| A、30° | B、60° |
| C、120° | D、150° |
已知函数y=f(x)+x是偶函数,且f(2)=3,则f(-2)=( )
| A、-7 | B、7 | C、-5 | D、5 |
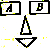 用黑、蓝2种颜色给如图所示的笑脸涂色,每个图形只能涂一种颜色,则两只眼睛(即图中A、B所示的区域)涂同种颜色而鼻子和嘴巴涂不同颜色的概率为( )
用黑、蓝2种颜色给如图所示的笑脸涂色,每个图形只能涂一种颜色,则两只眼睛(即图中A、B所示的区域)涂同种颜色而鼻子和嘴巴涂不同颜色的概率为( )
