题目内容
12.求证:函数f(x)=x+$\frac{a}{x}$(a>0)在($\sqrt{a}$,+∞)上是增函数.分析 根据函数单调性的定义利用定义法进行证明即可.
解答 解:任取x1,x2∈($\sqrt{a}$,+∞),且x1<x2,
则f(x1)-f(x2)=x1+$\frac{a}{{x}_{1}}$-x2-$\frac{a}{{x}_{2}}$=(x1-x2)+$\frac{a}{{x}_{1}}$-$\frac{a}{{x}_{2}}$=(x1-x2)+$\frac{a({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}$=(x1-x2)•$\frac{{x}_{1}{x}_{2}-a}{{x}_{1}{x}_{2}}$,
因为$\sqrt{a}$<x1<x2,
所以x1-x2<0,x2x1>$\sqrt{a}•\sqrt{a}$=a,
则x1x2-a>0,
所以f(x1)-f(x2)<0,
即函数f(x)=x+$\frac{a}{x}$(a>0)在($\sqrt{a}$,+∞)上是增函数.
点评 本题主要考查函数单调性的判断,利用函数单调性的定义是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知命题p:“若直线a与平面α内两条直线垂直,则直线a与平面α垂直”,命题q:“存在两个相交平面垂直于同一条直线”,则下列命题中的真命题为( )
| A. | p∧q | B. | p∨q | C. | ¬p∨q | D. | p∧¬q |
17.已知正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成角的余弦值为$\frac{1}{4}$.
16.过y2=2px焦点F的直线交抛物线于A,B,若|BF|=$\frac{6}{5}$,|AF|=$\frac{6}{7}$,则抛物线方程( )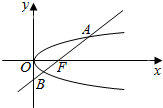

| A. | y2=x | B. | y2=2x | C. | y2=3x | D. | y2=4x |
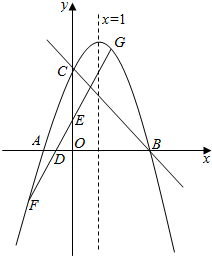 如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.
如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.