题目内容
函数y=2cos(3x+
)的图象可以先由y=cosx的图象向 平移 个单位,然后把所得的图象上所有点的横坐标 为原来的 倍(纵坐标不变)而得到,再将所得的图象上所有点的纵坐标 为原来的 倍(横坐标不变)而得到.
| π |
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:利用函数y=Asin(ωx+φ)的图象的平移变换与伸缩变换,即可求得答案.
解答:
解:依题意,函数y=2cos(3x+
)的图象先在x轴方向进行平移变换与伸缩变换:
将y=cosx的图象向左平移
个单位,然后把所得的图象上所有点的横坐标缩短为原来的
倍(纵坐标不变)而得到,
再在y轴方向进行平移变换与伸缩变换:将所得的图象上所有点的纵坐标伸长为原来的2倍(横坐标不变)而得到.
故答案为:左,
,缩短;
,伸长,2.
| π |
| 3 |
将y=cosx的图象向左平移
| π |
| 3 |
| 1 |
| 3 |
再在y轴方向进行平移变换与伸缩变换:将所得的图象上所有点的纵坐标伸长为原来的2倍(横坐标不变)而得到.
故答案为:左,
| π |
| 3 |
| 1 |
| 3 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查平移变换与伸缩变换的综合应用,属于中档题.

练习册系列答案
相关题目
 如图,已知F1、F2为椭圆的焦点,等边三角形AF1F2两边的中点M,N在椭圆上,则椭圆的离心率为( )
如图,已知F1、F2为椭圆的焦点,等边三角形AF1F2两边的中点M,N在椭圆上,则椭圆的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设a、b∈z,且a≠0,则(a-b)a2<0,且a<b的( )条件.
| A、充分不必要 |
| B、必要而不充分 |
| C、充要 |
| D、既不充分也不必要 |
直角坐标系中坐标原点O关于直线l:2xtanα+y-1=0的对称点为A(1,1),则tan2α的值为( )
A、-
| ||
B、
| ||
| C、1 | ||
D、
|
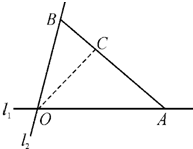 如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为75°.已知OC=(
如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为75°.已知OC=(