题目内容
19.已知函数f(x)=x+$\frac{1}{x}$.(I)判断函数的奇偶性,并加以证明;
(II)用定义证明f(x)在(0,1)上是减函数;
(III)函数f(x)在(-1,0)上的单调性如何?(直接写出答案,不要求写证明过程).
分析 (I)函数的定义域为{x|x≠0},直接利用奇偶性定义证明即可;
(II)直接利用函数单调性定义证明即可;
(III)根据函数的性质(I)(II)可直接得出结果;
解答 解:(I)由题意知:x≠0;
∴函数的定义域为{x|x≠0};
又∵$f(-x)=-x-\frac{1}{x}=-(x+\frac{1}{x})=-f(x)$;
∴函数f(x)为奇函数;
(II)设0<x1<x2<1则
$f({x_1})-f({x_2})={x_1}+\frac{1}{x_1}-{x_2}-\frac{1}{x_2}=({x_1}-{x_2})-\frac{{{x_1}-{x_2}}}{{{x_1}{x_2}}}=({x_1}-{x_2})(1-\frac{1}{{{x_1}{x_2}}})$;
∵0<x1<x2<1;
∴${x_1}-{x_2}<0,1-\frac{1}{{{x_1}{x_2}}}<0$;
∴f(x1)-f(x2)>0即f(x1)>f(x2);
∴函数f(x)在(0,1)上是减函数;
(III)函数f(x)在(-1,0)上是减函数.
点评 本题主要考查了函数的奇偶性定义、单调性定义证明等函数基本性质,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.如图,在平行四边形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{AN}=3\overrightarrow{NC}$,则$\overrightarrow{BN}$=( )
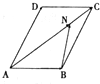

| A. | $\frac{3}{4}\overrightarrow b+\frac{1}{4}\overrightarrow a$ | B. | $\frac{1}{4}\overrightarrow b+\frac{3}{4}\overrightarrow a$ | C. | $\frac{3}{4}\overrightarrow b-\frac{1}{4}\overrightarrow a$ | D. | $\frac{1}{4}\overrightarrow b-\frac{3}{4}\overrightarrow a$ |
7.已知p是曲线$\left\{\begin{array}{l}{x=2cosβ}\\{y=\sqrt{3}sinβ}\end{array}\right.$上一点,F1,F2是该曲线的两个焦点,若△F1PF2内角平分线的交点到三边上的距离为1,则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | -$\frac{9}{4}$ | D. | 0 |
14.已知α,β是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足$\frac{1}{α}$+$\frac{1}{β}$=-1,则m的值是( )
| A. | 3或-1 | B. | 3 | C. | 1 | D. | -3或1 |
4.若数列{an}满足关系:an+1=1+$\frac{1}{a_n}$,a1=1,则a3=( )
| A. | $\frac{8}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{13}{8}$ |
11.若△ABC的内角A、B、C所对的边a、b、c满足(a+b)2-c2=4,且C=60°,则△ABC的面积为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$-3 | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
8.若a=30.6,b=log30.2,c=0.63,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<c<a | C. | a<b<c | D. | a<c<b |
9.设集合M={x|x=a},N={x|ax-1=0},若M∩N=N,则实数a的值为( )
| A. | 1或0 | B. | -1或0 | C. | 1或-1 | D. | 0或1或-1 |