题目内容
4.记${\left.{\overline{{a_n}{a_{n-1}}{a_{n-2}}…{a_1}{a_0}}}\right|_m}$=a0+a1×m+…+an-1×mn-1+an×mn,其中n≤m,m、n均为正整数,ak∈{0,1,2,…,m-1}(k=0,1,2,…,n)且an≠0;(1)计算${\left.{\overline{2016}}\right|_7}$=699;
(2)设集合A(m,n)=$\left\{{{{\left.{\left.x\right|x=\overline{{a_n}{a_{n-1}}{a_{n-2}}…{a_1}{a_0}}}\right|}_m}}\right\}$,则A(m,n)中所有元素之和为$\frac{{({{m^{n+1}}+{m^n}-1})({{m^{n+1}}-{m^n}})}}{2}$.
分析 (1)${\left.{\overline{2016}}\right|_7}$=6+1×7+2×73=699;
(2)分别求出含有a1、…、an-1,an的项共有m•mn-1(m-1)项及和,即可得出结论.
解答 解:(1)${\left.{\overline{2016}}\right|_7}$=6+1×7+2×73=699;
(2)由题意,a0、a1、…、an-1,各有m种取法,an有m-1中取法.
a0=0,1,2,…m-1时,a1、…、an-1,各有m种取法,an有m-1中取法,
所以含有a0的项共有mn-1(m-1)项,和为(0+1+2+…+m-1)mn-1(m-1)=$\frac{m(m-1)}{2}$mn-1(m-1),
同理a1=0,1,2,…m-1时,a0、a2、…、an-1,各有m种取法,an有m-1中取法,
所以含有a1的项共有m•mn-1(m-1)项,和为(0+1+2+…+m-1)mn-1(m-1)=$\frac{m(m-1)}{2}$m•mn-1(m-1),
…
an=1,2,…m-1时,a0、a1、…、an-1,各有m种取法,
所以含有an的项共有mn•mn项,和为(1+2+…+m-1)mn•mn=$\frac{m(m-1)}{2}$•mn•mn,
所以所有元素之和为$\frac{m(m-1)}{2}$mn-1(m-1)(1+m+…+mn)+$\frac{m(m-1)}{2}$mnmn=$\frac{{({{m^{n+1}}+{m^n}-1})({{m^{n+1}}-{m^n}})}}{2}$.
故答案为:699;$\frac{{({{m^{n+1}}+{m^n}-1})({{m^{n+1}}-{m^n}})}}{2}$.
点评 本题考查新定义,考查数列的求和公式,考查学生分析解决问题的能力,难度大.


| A. | $\frac{16\sqrt{2}}{3}$cm3 | B. | $\frac{32}{3}$cm3 | C. | 16$\sqrt{2}$cm3 | D. | 32cm3 |
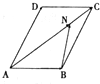
| A. | $\frac{3}{4}\overrightarrow b+\frac{1}{4}\overrightarrow a$ | B. | $\frac{1}{4}\overrightarrow b+\frac{3}{4}\overrightarrow a$ | C. | $\frac{3}{4}\overrightarrow b-\frac{1}{4}\overrightarrow a$ | D. | $\frac{1}{4}\overrightarrow b-\frac{3}{4}\overrightarrow a$ |
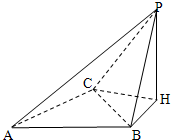 如图,在四面体P-ABC,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.
如图,在四面体P-ABC,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.