题目内容
17.已知:数列{an},{bn}中,a1=0,b1=1,且当n∈N*时,an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列;(1)求数列{an},{bn}的通项公式;
(2)求最小自然数k,使得当n≥k时,对任意实数λ∈[0,1],不等式(2λ-3)bn≥(2λ-4)an+λ-3恒成立.
分析 (1)由当n∈N*时,an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列;可得2bn=an+an+1,${a}_{n+1}^{2}$=bnbn+1.又a1=0,b1=1,an,bn≥0,且2bn=$\sqrt{{b}_{n}{b}_{n-1}}$+$\sqrt{{b}_{n}{b}_{n+1}}$,即$2\sqrt{{b}_{n}}$=$\sqrt{{b}_{n-1}}$+$\sqrt{{b}_{n+1}}$(n≥2)利用等差数列的通项公式即可得出.
(2)把bn,an代入不等式(2λ-3)bn≥(2λ-4)an+λ-3,整理可得:(2n-1)λ+n2-4n+3≥0,令f(λ)=(2n-1)λ+n2-4n+3,利用一次函数的单调性可得:$\left\{\begin{array}{l}{f(0)≥0}\\{f(1)≥0}\end{array}\right.$,解出即可得出.
解答 解:(1)∵当n∈N*时,an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列;
∴2bn=an+an+1,${a}_{n+1}^{2}$=bnbn+1.又∵a1=0,b1=1,∴an,bn≥0,且2bn=$\sqrt{{b}_{n}{b}_{n-1}}$+$\sqrt{{b}_{n}{b}_{n+1}}$,
∴$2\sqrt{{b}_{n}}$=$\sqrt{{b}_{n-1}}$+$\sqrt{{b}_{n+1}}$(n≥2),∴数列{bn}是等差数列,又b2=4,∴$\sqrt{{b}_{n}}$=n,n=1时也适合.
∴bn=n2,an=n(n-1).
(2)把bn,an代入不等式(2λ-3)bn≥(2λ-4)an+λ-3,整理可得:(2n-1)λ+n2-4n+3≥0,
令f(λ)=(2n-1)λ+n2-4n+3,利用一次函数的单调性可得:$\left\{\begin{array}{l}{f(0)≥0}\\{f(1)≥0}\end{array}\right.$,∴$\left\{\begin{array}{l}{{n}^{2}-4n+3≥0}\\{{n}^{2}-2n+2≥0}\end{array}\right.$,
解得n≤1,或n≥3.
∴存在自然数k=3,使得当n≥k时,对任意实数λ∈[0,1],不等式(2λ-3)bn≥(2λ-4)an+λ-3恒成立.
点评 本题考查了等差数列与等比数列的通项公式、一次函数的单调性、不等式的解法,考查了推理能力与计算能力,属于中档题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案| 优秀 | 非优秀 | |
| 喜欢 | 10 | 50 |
| 不喜欢 | 20 | 30 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(2)现采用分层抽样方法,从不喜欢的样本中抽取5人,再从5人中随机抽取2人,求至少有一人成绩优秀的概率.
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |

| A. | $\frac{16\sqrt{2}}{3}$cm3 | B. | $\frac{32}{3}$cm3 | C. | 16$\sqrt{2}$cm3 | D. | 32cm3 |
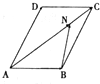
| A. | $\frac{3}{4}\overrightarrow b+\frac{1}{4}\overrightarrow a$ | B. | $\frac{1}{4}\overrightarrow b+\frac{3}{4}\overrightarrow a$ | C. | $\frac{3}{4}\overrightarrow b-\frac{1}{4}\overrightarrow a$ | D. | $\frac{1}{4}\overrightarrow b-\frac{3}{4}\overrightarrow a$ |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | -$\frac{9}{4}$ | D. | 0 |