题目内容
甲、乙两人进行了八十一回合的某类型球赛，两人先抽签决定第一回合的发球权，之后的回合则由两人轮流发球，比赛结果甲以2：1的比率获胜，且在八十一回合中，共有四十一回合不是发球者获胜．请问第一回合的发球者在所有他发球的回合中共赢了几回合？
考点：概率的意义
专题：概率与统计
分析：由于甲、乙两人进行了八十一回合的某类型球赛，比赛结果甲以2：1的比率获胜，可得甲共获胜
×81=54场，乙共获胜27场．
①假设甲是第一回合的发球者，乙是第二回合的发球者．则甲在41场中发球共获胜x场，乙在40场中发球共获胜y场，由于在八十一回合中，共有四十一回合不是发球者获胜．可得x+y=40，41-x+y=27，解得x．
②假设乙是第一回合的发球者，甲是第二回合的发球者．同理即可推断出．
| 2 |
| 3 |
①假设甲是第一回合的发球者，乙是第二回合的发球者．则甲在41场中发球共获胜x场，乙在40场中发球共获胜y场，由于在八十一回合中，共有四十一回合不是发球者获胜．可得x+y=40，41-x+y=27，解得x．
②假设乙是第一回合的发球者，甲是第二回合的发球者．同理即可推断出．
解答：
解：由于甲、乙两人进行了八十一回合的某类型球赛，比赛结果甲以2：1的比率获胜，
因此甲共获胜
×81=54场，乙共获胜27场．
①假设甲是第一回合的发球者，乙是第二回合的发球者．
则甲在第1，3，…，81场中发球共获胜x场，乙在第2，4，…，80场中发球共获胜y场，
由于在八十一回合中，共有四十一回合不是发球者获胜．
因此x+y=40，41-x+y=27，解得x=27．
当甲是第一回合的发球者时，在所有他发球的回合中共赢了27回合．
②假设乙是第一回合的发球者，甲是第二回合的发球者．
则乙在第1，3，…，81场中发球共获胜x场，甲在第2，4，…，80场中发球共获胜y场，
由于在八十一回合中，共有四十一回合不是发球者获胜．
因此x+y=40，41-x+y=54，解得y=
，不符合题意一个舍去．
综上①②可得：只能是：甲是第一回合的发球者，在所有他发球的回合中共赢了27回合．
因此甲共获胜
| 2 |
| 3 |
①假设甲是第一回合的发球者，乙是第二回合的发球者．
则甲在第1，3，…，81场中发球共获胜x场，乙在第2，4，…，80场中发球共获胜y场，
由于在八十一回合中，共有四十一回合不是发球者获胜．
因此x+y=40，41-x+y=27，解得x=27．
当甲是第一回合的发球者时，在所有他发球的回合中共赢了27回合．
②假设乙是第一回合的发球者，甲是第二回合的发球者．
则乙在第1，3，…，81场中发球共获胜x场，甲在第2，4，…，80场中发球共获胜y场，
由于在八十一回合中，共有四十一回合不是发球者获胜．
因此x+y=40，41-x+y=54，解得y=
| 53 |
| 2 |
综上①②可得：只能是：甲是第一回合的发球者，在所有他发球的回合中共赢了27回合．
点评：本题考查了概率的意义、分类讨论的思想方法，考查了方程的思想解决问题，考查了推理能力与计算能力，属于难题．
练习册系列答案
一课一练课时达标系列答案
相关题目
数列（an），（bn）是等差数列，Tn、Sn分别是数列（an），（bn）的前n项和，且
=
，则
=（ ）
| Sn |
| Tn |
| n |
| 2n-1 |
| a6 |
| b6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
用二分法求函数f（x）=x3+x2-2x-2的一个零点，依次计算得到如表函数值：
那么方程x3+x2-2x-2=0的一个近似根在下列哪两数之间（ ）
| f（1）=-2 | f（1.5）=0.625 |
| f（1.25）=-0.984 | f（1.375）=-0.260 |
| f（1.438）=0.165 | f（1.4065）=-0.052 |
| A、1.25～1.375 |
| B、1.375～1.4065 |
| C、1.4065～1.438 |
| D、1.438～1.5 |
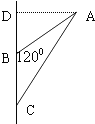在△ABC中，AB=2，BC=1.5，∠ABC=120°（如图），若将△ABC绕直线BC旋转一周，则所形成的旋转体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=3sin（2x+
）的一条对称轴方程为（ ）
| π |
| 3 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
