题目内容
如图所示,三棱锥M,PA⊥底面ABC,∠ABC=90°,则此三棱锥P-ABC中直角三角形有 个.
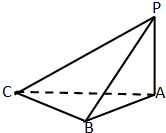

考点:棱锥的结构特征
专题:空间位置关系与距离
分析:由已知,得到直角三角形ABC,ABP,ACP,只要再判断三角形PBC的现状即可.
解答:
解:由已知PA⊥底面ABC,∠ABC=90°,
所以CB⊥PA,CB⊥AB,又PA∩AB=A,
所以CB⊥平面PAB,
所以CB⊥PB,
所以此三棱锥P-ABC中直角三角形有△ABC,△ABP,△ACP,△PBC共有4个.
故答案为:4.
所以CB⊥PA,CB⊥AB,又PA∩AB=A,
所以CB⊥平面PAB,
所以CB⊥PB,
所以此三棱锥P-ABC中直角三角形有△ABC,△ABP,△ACP,△PBC共有4个.
故答案为:4.
点评:本题考查了线面垂直的判定定理和性质定理的运用,关键是熟练线面垂直的判定定理和性质定理,属于基础题.

练习册系列答案
相关题目
下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,则能得出AB∥平面MNP的图形个数是( )
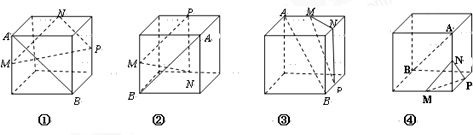

| A、1个 | B、2个 | C、3个 | D、4个 |
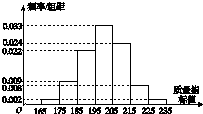 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.