题目内容
已知点P(x,y)是圆x2+y2-6x-4y+12=0上的动点,求:
(1)x2+y2的最值;
(2)x+y的最值;
(3)P到直线x+y-1=0的距离d的最值.
(1)x2+y2的最值;
(2)x+y的最值;
(3)P到直线x+y-1=0的距离d的最值.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)设z=x2+y2,利用z的几何意义即可得到结论;
(2)设z=x+y,利用z的几何意义即可得到结论
(3)根据点到直线的距离公式即可得到结论.
(2)设z=x+y,利用z的几何意义即可得到结论
(3)根据点到直线的距离公式即可得到结论.
解答:
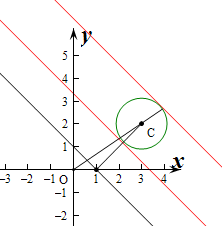
解:x2+y2-6x-4y+12=0的标准方程为(x-3)2+(y-2)2=1,圆心为C(3,2),半径r=1,
(1)设z=x2+y2,则z的几何意义为圆上点到原点的距离的平方,
 原点到圆心的距离d=
原点到圆心的距离d=
=
,
∴圆上的点到原点的最大距离为
+1,最小距离为
-1,
则z的最大值为(
+1)2=14+2
,
z的最大值为(
-1)2=14-2
.
(2)设z=x+y,即x+y-z=0,
在圆心C到直线x+y-z=0的距离满足d≤r,
即
≤1,
即|z-5|≤
,
解得5-
≤z≤5+
,
即x+y的最大值为5+
,最小值为5-
.
(3)圆心到直线x+y-1=0的距离d=
=
=2
>1,
∴直线和圆相离,
∴P到直线x+y-1=0的距离d的最大值2
+1,
d的最小值为2
-1.
(1)设z=x2+y2,则z的几何意义为圆上点到原点的距离的平方,
 原点到圆心的距离d=
原点到圆心的距离d=| 32+22 |
| 13 |
∴圆上的点到原点的最大距离为
| 13 |
| 13 |
则z的最大值为(
| 13 |
| 13 |
z的最大值为(
| 13 |
| 13 |
(2)设z=x+y,即x+y-z=0,
在圆心C到直线x+y-z=0的距离满足d≤r,
即
| |3+2-z| | ||
|
即|z-5|≤
| 2 |
解得5-
| 2 |
| 2 |
即x+y的最大值为5+
| 2 |
| 2 |
(3)圆心到直线x+y-1=0的距离d=
| |3+2-1| | ||
|
| 4 | ||
|
| 2 |
∴直线和圆相离,
∴P到直线x+y-1=0的距离d的最大值2
| 2 |
d的最小值为2
| 2 |
点评:本题主要考查直线和圆的位置关系,点与圆的位置关系以及两点间的距离公式,点到直线的距离公式的应用,考查学生的计算能力立意数形结合是解决本题的关键.本题也可以使用三角换元法进行求解.

练习册系列答案
相关题目
数列6,9,14,21,30,…的一个通项公式是( )
| A、3n+3 |
| B、2n2+1 |
| C、2n+n+3 |
| D、n2+5 |
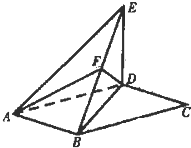 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4;将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4;将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.