题目内容
10.“若f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2,…,xn,有$\frac{1}{n}[{f({x_1})+f({x_2})++f(x_n^{\;})}]≤f(\frac{{{x_1}+{x_2}++{x_n}}}{n})$”设f(x)=sinx在(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值是( )| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 运用是凸函数的定义,可得$\frac{1}{3}$[f(A)+f(B)+f(C)]≤f($\frac{A+B+C}{3}$),计算即可得到所求最大值,及等号成立的条件.
解答 解:由f(x)=sinx在(0,π)上是凸函数,
可得在△ABC中,$\frac{1}{3}$[f(A)+f(B)+f(C)]≤f($\frac{A+B+C}{3}$),
即有$\frac{1}{3}$(sinA+sinB+sinC)≤sin$\frac{π}{3}$,
即sinA+sinB+sinC≤3sin$\frac{π}{3}$=$\frac{3\sqrt{3}}{2}$.
当且仅当A=B=C=$\frac{π}{3}$时,取得等号.
则sinA+sinB+sinC的最大值是$\frac{3\sqrt{3}}{2}$.
故选:C.
点评 本题考查新定义的理解和运用,同时考查三角形的内角和定理,考查运算能力,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
20.已知集合A={1,2,3,4,5},B={x∈Z|x≤2},则A∩B中的元素个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.设集合A={x|(x-3)(x-1)>0},B={x|y=lg(2x-3)},则A∩B=( )
| A. | $[\frac{3}{2},3)$ | B. | (3,+∞) | C. | $(1,\frac{3}{2})$ | D. | ($\frac{3}{2}$,3) |
18.已知互不重合的直线l,m,互不重合的平面α,β,给出下列四个命题,错误的命题是( )
| A. | 若l∥α,l∥β,α∩β=m,则l∥m | B. | 若α⊥β,l⊥α,m⊥β则l⊥m | ||
| C. | 若α⊥β,α⊥γ,β∩γ=l,则l⊥α | D. | 若α∥β,l∥α,则l∥β |
2.已知$\overrightarrow a=({1,2}),\overrightarrow b=({m,1})$,若$\overrightarrow a⊥\overrightarrow b$,则m=( )
| A. | $-\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
19.若f(x)=sin3x+acos2x在(0,π)上存在最小值,则实数a的取值范围是( )
| A. | (0,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (0,+∞) |
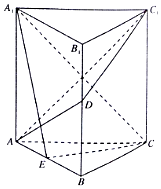 如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D为棱BB1上一点,E是AB的中点.
如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D为棱BB1上一点,E是AB的中点.