题目内容
19.若f(x)=sin3x+acos2x在(0,π)上存在最小值,则实数a的取值范围是( )| A. | (0,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (0,+∞) |
分析 设t=sinx,由x∈(0,π)和正弦函数的性质求出t的范围,将t代入f(x)后求出函数的导数,求出临界点,根据条件判断出函数的单调性,由导数与函数单调性的关系列出不等式,求出实数a的取值范围.
解答 解:设t=sinx,由x∈(0,π)得t∈(0,1],
∵f(x)=sin3x+acos2x=sin3x+a(1-sin2x),
∴f(x)变为:y=t3-at2+a,
则y′=3t2-2at=t(3t-2a),
由y′=0得,t=0或t=$\frac{2a}{3}$,
∵f(x)=sin3x+acos2x在(0,π)上存在最小值,
∴函数y=t3-at2+a在(0,1]上递减或先减后增,
即$\frac{2a}{3}$>0,得a>0,
∴实数a的取值范围是(0,+∞),
故选:D.
点评 本题考查正弦函数的性质,导数与函数单调性的关系,以及构造法、换元法的应用,考查化简、变形能力.

练习册系列答案
相关题目
9.直线xcosα+$\sqrt{3}$y+2=0的倾斜角的取值范围( )
| A. | [0,$\frac{5π}{6}$] | B. | [$\frac{π}{6}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{5π}{6}$] | C. | [$\frac{π}{6}$,$\frac{5π}{6}$] | D. | [0,$\frac{π}{6}$]∪[$\frac{5π}{6}$,π) |
10.“若f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2,…,xn,有$\frac{1}{n}[{f({x_1})+f({x_2})++f(x_n^{\;})}]≤f(\frac{{{x_1}+{x_2}++{x_n}}}{n})$”设f(x)=sinx在(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值是( )
| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
7.双曲线$\frac{x^2}{16}-\frac{y^2}{9}=-1$的渐近线方程为( )
| A. | $y=±\frac{3}{4}x$ | B. | $y=±\frac{4}{3}x$ | C. | $y=±\frac{16}{9}x$ | D. | $y=±\frac{9}{16}x$ |
11.已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.右面是一个算法的程序框图,当输入n的值为12时,则输出的结果为( )
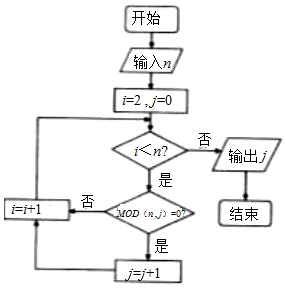

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$表示的点集M,不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{y≥2{x}^{2}}\end{array}\right.$表示的点集记为N,在M中任取一点P,则P∈N的概率为( )
| A. | $\frac{5}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{16}$ | D. | $\frac{5}{16}$ |