题目内容
15．已知复数x满足x+$\frac{1}{x}$=-1，则x2013+$\frac{1}{{{x^{2013}}}}$=2．分析 由题意可得x3=1，因为2013能够被3整除，所以x2013=1，问题得以解决．
解答 解：∵$x+\frac{1}{x}=-1$，
∴x2+x+1=0，
∴（x-1）（x2+x+1）=x3-1=0，
∴x3=1，
∵2013能够被3整除，
∴x2013=1，
∴x2013+$\frac{1}{{{x^{2013}}}}$=1+1=2，
故答案为：2
点评 本题考查了方程的解得问题，以及指数幂的运算，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
6．下列表示正确的是（ ）
| A． | {1}∈{1，3} | B． | 1⊆{1，2} | C． | ∅∈{0} | D． | ∅⊆∅ |
3．已知集合A={ x|$\frac{1}{x-1}$≥1}，集合B={ x|log2x＜1}，则 A∩B=（ ）
| A． | （-∞，2） | B． | （0，1） | C． | （0，2） | D． | （1，2） |
10．“若f（x）在区间D上是凸函数，则对于区间D内的任意x1，x2，…，xn，有$\frac{1}{n}[{f（{x_1}）+f（{x_2}）++f（x_n^{\;}）}]≤f（\frac{{{x_1}+{x_2}++{x_n}}}{n}）$”设f（x）=sinx在（0，π）上是凸函数，则在△ABC中，sinA+sinB+sinC的最大值是（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{{3\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
7．双曲线$\frac{x^2}{16}-\frac{y^2}{9}=-1$的渐近线方程为（ ）
| A． | $y=±\frac{3}{4}x$ | B． | $y=±\frac{4}{3}x$ | C． | $y=±\frac{16}{9}x$ | D． | $y=±\frac{9}{16}x$ |
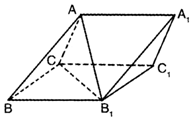如图，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，AC=AB1．