题目内容

已知A={x|ax2-2x-1=0}，如果A∩R+=∅，求a的取值．
考点：交集及其运算
专题：集合
分析：根据A∩R+=∅判定集合A的解，集合A中有字母，要讨论．
解答： 解1°若a=0　则A={-
1
2
}　满足A∩R+=∅
2°若a≠0时
（1）△=4+4a＜0时即a＜-1　A=∅满足A∩R+=∅
（2）△≥0即a≥-1要A∩R+=∅只须
△≥0
2
a
＜0
-
1
a
＞0
，解得：-1≤a＜0，
综上所述a的取值范围为 {a|a≤0}．
点评：本题主要考查集合的运算，属于基础题．
练习册系列答案
相关题目
已知函数f（x）的定义域为（-∞，-1）∪（1，+∞），对定义域内的任意x，满足f（x）+f（-x）=0，当x＜-1时，f（x）=
1+ln(-x-1)
x+a
（a为常数），且x=2是函数f（x）的一个极值点．
（Ⅰ）若x≥2时，f（x）≥
m
x
，求实数m的取值范围；
（Ⅱ）求证：n-2（
1
2
+
2
3
+
3
4
+…+
n
n+1
）＜ln（n+1）．
已知A（2，3），B（5，4），C（7，10），若点P满足
AP
=
AB
+λ
AC
，
（1）当λ为何值时，点P在直线y=x上；
（2）当λ范围是多少时，点P在第三象限．
三角比内容丰富，公式很多．若仔细观察、大胆猜想、科学求证，你也能发现其中的一些奥秘．请你完成以下问题：
（1）计算：
cos2°
sin47°
+
cos88°
sin133°
=
 
；
cos5°
sin50°
+
cos85°
sin130°
=
 
；
cos12°
sin57°
+
cos78°
sin123°
=
 
．
（直接写答案，别忘记把计算器设置成“角度”！）
（2）根据（1）的计算结果，请你猜出一个一般性的结论：
 
．（用数学式子加以表达，并证明你的结论，写出推理过程．）
已知函数f（x）=
3
sinωxcosωx+cos2ωx+
1
2
（ω＞0，x∈R）的最小正周期为π．
（Ⅰ）求ω的值；
（Ⅱ）求函数f（x）在区间[0，
π
2
]上的取值范围．
求下列各式的值．
（1）
1
2
lg25+lg2-lg
0.1
-log29×log32；
（2）
lg25+lg2•lg50+(lg2)2
．
化简下列式子
（1）（2a 
2
3
b 
1
2
）•（-
3
a 
1
4
b 
1
2
）÷（3a 
1
6
b 
5
6
）
（2）
lg8+lg125-lg2-lg5
lg
10
•lg0.1
-log54×log45-log0.51．
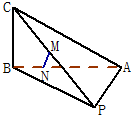已知三棱锥P-ABC中，PA=PB，CB⊥平面PAB，PM=MC，AN=3NB．
（1）求证明：MN⊥AB；
（2）当∠APB=90°，BC=2，AB=4时，求MN的长．
里氏震级M的计算公式为：M=lgA-lgA0，其中A是测震仪记录的地震曲线的最大振幅，A0是相应的标准地震的振幅，假设在一次地震中，测震仪记录的最大振幅是100000，此时标准地震的振幅为0.001，则此次地震的震级为
 
级．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网