题目内容
曲线y=x3和y=x
所围成的封闭图形的面积是 .
| 1 |
| 3 |
考点:定积分在求面积中的应用
专题:导数的综合应用
分析:作出函数图象,求出交点坐标,利用积分的几何意义,求面积即可
解答:
解:作出两个函数的图象如图:
由
,得
或
,
即A(1,1),B(-1,-1),
由函数的对称性和积分的几何意义可知所围成的封闭图形的面积为:
2
(x
-x3)dx=2(
x
-
x4)|
=2(
-
)=1,
故答案为:1.

由
|
|
|
即A(1,1),B(-1,-1),
由函数的对称性和积分的几何意义可知所围成的封闭图形的面积为:
2
| ∫ | 1 0 |
| 1 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| 4 |
1 0 |
| 3 |
| 4 |
| 1 |
| 4 |
故答案为:1.
点评:本题主要考查利用积分的几何意义求区域面积,根据图象求出函数图象的交点,要求熟练掌握常见函数的积分公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
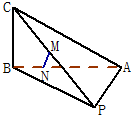 已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.
已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.