题目内容
6.已知sinα=$\frac{12}{13}$,并且α是第二象限角,则tan$\frac{α}{2}$的值为$\frac{3}{2}$.分析 由条件利用同角三角的基本关系求得tanα的值,再利用二倍角的正切公式求得tan$\frac{α}{2}$的值.
解答 解:∵sinα=$\frac{12}{13}$,并且α是第二象限角,
∴cosx=-$\sqrt{{1-sin}^{2}α}$=-$\frac{5}{13}$,∴tanα=$\frac{sinα}{cosα}$=-$\frac{12}{5}$.
由2kπ+$\frac{π}{2}$<α<2kπ+π,求得kπ+$\frac{π}{4}$<$\frac{α}{2}$<kπ+$\frac{π}{2}$,
故$\frac{α}{2}$是第一或第三象限角,∴tan$\frac{α}{2}$>1.
再根据 tanα=-$\frac{12}{5}$=$\frac{2tan\frac{α}{2}}{1{-tan}^{2}\frac{α}{2}}$,求得tan$\frac{α}{2}$=$\frac{3}{2}$ 或 tan$\frac{α}{2}$=-$\frac{2}{3}$(舍去),
故答案为:$\frac{3}{2}$.
点评 本题主要考查同角三角的基本关系,二倍角的正切公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知集合A={x|2x<2},B={y|y=$\sqrt{x}$},则A∩B=( )
| A. | [0,1) | B. | (0,2) | C. | (1,+∞) | D. | [0,+∞) |
1.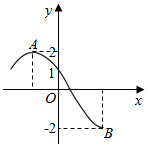 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
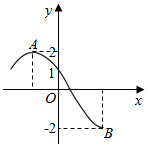 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )| A. | -1 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 1 |
11.已知集合A={x|y=ln(x-1)},集合B={x|x2-3x>0},则A∩(∁RB)=( )
| A. | (1,3) | B. | (1,3] | C. | [0,+∞) | D. | [3,+∞) |