题目内容
13.若x>0,求函数y=x+$\frac{4}{x}$的最小值,并求此时x的值.分析 由于x>0,利用基本不等式可得y=x+$\frac{4}{x}$≥2=4,满足等号成立的条件,于是问题解决.
解答 解:∵x>0,
∴y=x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,当且仅当x=$\frac{4}{x}$,即x=2时取“=”.
故y=x+$\frac{4}{x}$的最小值为4,当x=2时,有最小值.
点评 本题考查基本不等式,关键是分析等号成立的条件,属于基础题.

练习册系列答案
相关题目
1.某空间几何体的三视图如图所示,则该几何体的体积为( )


| A. | 128 | B. | $\frac{128}{3}$ | C. | $\frac{64}{3}$ | D. | $\frac{32}{3}$ |
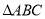 中,
中,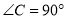 ,点
,点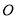 在
在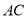 上,以
上,以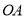 为半径的
为半径的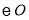 交
交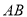 于点
于点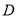 ,
,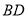 的垂直平分线交
的垂直平分线交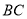 于点
于点 ,交
,交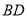 于点
于点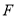 ,连接
,连接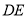 .
.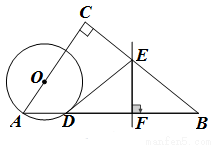
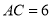 ,
,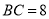 ,
, ,求线段
,求线段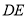 的长.
的长.