题目内容
1.某空间几何体的三视图如图所示,则该几何体的体积为( )
| A. | 128 | B. | $\frac{128}{3}$ | C. | $\frac{64}{3}$ | D. | $\frac{32}{3}$ |
分析 几何体为直三棱柱切去一个小三棱锥得到的,使用作差法求出其体积.
解答  解:由三视图可知几何体为直三棱柱ABC-A′B′C′切去三棱锥C′-CA′B′剩余的部分
解:由三视图可知几何体为直三棱柱ABC-A′B′C′切去三棱锥C′-CA′B′剩余的部分
其中直三棱柱的底面ABC是直角三角形,AC⊥BC,AC=BC=CC′=4.
∴几何体的体积V=$\frac{1}{2}×4×4×4-\frac{1}{3}×\frac{1}{2}×4×4×4$=$\frac{64}{3}$.
故选C.
点评 本题考查了常见几何体的三视图和体积计算,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
17.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{9}$=1有( )
| A. | 相同短轴 | B. | 相同长轴 | C. | 相同离心率 | D. | 以上都不对 |
11.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,在双曲线C上存在点P,满足△PF1F2的周长等于双曲线C的实轴长的3倍,则双曲线C的离心率的取值范围是( )
| A. | (1,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$) | C. | (1,$\frac{5}{2}$) | D. | (0,$\frac{5}{2}$) |
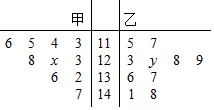 在某校统考中,甲、乙两班数学学科前10名的成绩如表:
在某校统考中,甲、乙两班数学学科前10名的成绩如表: