题目内容
18.把函数y=f(x)的图象向右平移$\frac{π}{6}$个单位,得到$y=2sin(3x-\frac{π}{4})$的图象,则函数y=f(x)的解析式是y=2sin(3x+$\frac{π}{4}$).分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由题意可得,把函数$y=2sin(3x-\frac{π}{4})$的图象向左平移$\frac{π}{6}$个单位后得到函数y=f(x)=2sin[3(x+$\frac{π}{6}$)-$\frac{π}{4}$]=2sin(3x+$\frac{π}{4}$)的图象,
故答案为:y=2sin(3x+$\frac{π}{4}$).
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下表给出了从某校500名12岁的男生中用简单随机抽样得出的120人的身高资料(单位:厘米):
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计身高低于134厘米的人数占总人数的百分比和身高在区间[134,146)(厘米)内的人数占总人数的百分比.
| 区间界限 | [122,126) | [126,130) | [130,134) | [134,138) | [138,142) |
| 人数 | 5 | 8 | 10 | 22 | 33 |
| 区间界限 | [142,146) | [146,150) | [150,154) | [154,158) | |
| 人数 | 20 | 11 | 6 | 5 |
(2)画出频率分布直方图;
(3)估计身高低于134厘米的人数占总人数的百分比和身高在区间[134,146)(厘米)内的人数占总人数的百分比.
7.f(x)=cosx-sinx在下列哪个区间上是单调递减的( )
| A. | $[{\frac{π}{4},\frac{5π}{4}}]$ | B. | [-π,0] | C. | [0,π] | D. | $[{0,\frac{π}{4}}]$ |
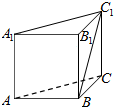 如图,直三棱柱ABC-A1B1C1中(侧棱垂直于底面),∠ABC=90°,且AB=BC=AA1,则BC1与面ACC1A1所成的角的大小为30°.
如图,直三棱柱ABC-A1B1C1中(侧棱垂直于底面),∠ABC=90°,且AB=BC=AA1,则BC1与面ACC1A1所成的角的大小为30°.