题目内容

抛物线y2=4x的焦点坐标为（　　）
A、（2，0）
B、（1，0）
C、（0，-4）
D、（-2，0）
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：先确定焦点位置，即在x轴正半轴，再求出P的值，可得到焦点坐标．
解答： 解：∵抛物线y2=4x是焦点在x轴正半轴的标准方程，
由2p=4得：p=2，
∴焦点坐标为：（1，0）
故选：B
点评：本题主要考查抛物线的焦点坐标．熟练掌握抛物线的基本性质是解答的关键，属基础题．
练习册系列答案
相关题目
在数列{an}中，an=（-1）n（2n+1）（n∈N+），则a1+a2+a3+…+a2012=
 
．
从1到k这k个整数中最少应选m个数才能保证选出的m个数中必存在三个不同的数可构成一个三角形的三边长．（1）若k=10，则m=
 
；
（2）若k=2012，则m=
 
．
在正四面体ABCD中，P，Q，R分别为所在棱的中点，则四面体过P，Q，R三点的截面图形为
 
．
双曲线
x2
16
-
y2
9
=1上到定点（5，0）的距离是9的点的个数是（　　）
A、0个B、2个C、3个D、4个．
求函数y=2sin（
1
2
x-
π
6
）的最值及取得最值时的x的取值集合，以及单调增区间．
若函数f（x）=
1
3
x3-x在（a，10-a2）上有最小值，则a的取值范围为
 
．
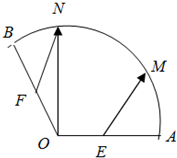如图，扇形OAB的半径OA=2，∠AOB=120°，点E是OA的中点，点F是OB的中点，点M，N分别是
AB
上靠近点A与点B的四等分点．求：
（1）
OB
•
ON
；
（2）
EM
•
FN
．
已知α∈（-
π
2
，
π
2
），且sin2α=cos（α-
π
4
），求α．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网