题目内容
5．已知α∈（$\frac{π}{2}$，π），sin（π-α）=$\frac{3}{5}$，则cosα等于（ ）| A． | $\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | -$\frac{4}{5}$ | D． | $\frac{4}{5}$ |
分析 先利用诱导公式求出sinα=$\frac{3}{5}$，α在第二象限，得cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$．
解答 解：sin（π-α）=$\frac{3}{5}$，
sinα=$\frac{3}{5}$，α∈（$\frac{π}{2}$，π），
cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$，
故答案选：C．
点评 本题考查诱导公式及同角三角函数的基本关系，属于基础题．
练习册系列答案
相关题目
15．
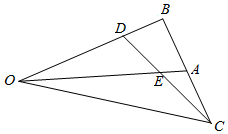如图：已知，在△OAB中，点A是BC的中点，点D是将向量$\overrightarrow{OB}$分为2：1的一个分点，DC和OA交于点E，则AO与OE的比值是（ ）
如图：已知，在△OAB中，点A是BC的中点，点D是将向量$\overrightarrow{OB}$分为2：1的一个分点，DC和OA交于点E，则AO与OE的比值是（ ）| A． | 2 | B． | $\frac{5}{4}$ | C． | $\frac{3}{2}$ | D． | $\frac{6}{5}$ |
20．设$\overrightarrow{a}$=（2，-3），$\overrightarrow{b}$=（x，2x），且3$\overrightarrow{a}$•$\overrightarrow{b}$=4，则x等于（ ）
| A． | -3 | B． | 3 | C． | -$\frac{1}{3}$ | D． | $\frac{1}{3}$ |
14．已知3tan$\frac{α}{2}$+$ta{n}^{2}\frac{α}{2}$=1，sinβ=3sin（2α+β），则tan（α+β）=（ ）
| A． | $\frac{4}{3}$ | B． | -$\frac{4}{3}$ | C． | -$\frac{2}{3}$ | D． | -3 |