题目内容
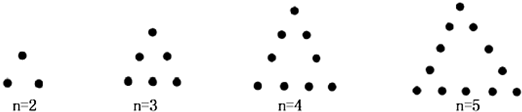
如图所示将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>1,n∈N)个点,相应的图案中总的点数记为an,则
+
+
+…+
= .
| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2013a2014 |

考点:归纳推理
专题:
分析:根据题意,可得a2=3=3×(2-1),a3=6=3×(3-1),a4=9=3×(4-1),a5=12=3×(5-1)…an=3(n-1),数列{an}是首项为3,公差为3的等差数列,通项为an=3(n-1)(n≥2);所以
=
=
(
-
),据此解答即可.
| 1 |
| anan+1 |
| 1 |
| 3(n-1)•3n |
| 1 |
| 9 |
| 1 |
| n-1 |
| 1 |
| n |
解答:
解:根据分析,可得
a2=3=3×(2-1),a3=6=3×(3-1),a4=9=3×(4-1),a5=12=3×(5-1)…an=3(n-1),
数列{an}是首项为3,公差为3的等差数列,通项为an=3(n-1)(n≥2);
所以
=
=
(
-
)
则
+
+
+…+
=9×
×(1-
+
-
+…+
-
)
=1-
=
故答案为:
.
a2=3=3×(2-1),a3=6=3×(3-1),a4=9=3×(4-1),a5=12=3×(5-1)…an=3(n-1),
数列{an}是首项为3,公差为3的等差数列,通项为an=3(n-1)(n≥2);
所以
| 1 |
| anan+1 |
| 1 |
| 3(n-1)•3n |
| 1 |
| 9 |
| 1 |
| n-1 |
| 1 |
| n |
则
| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2013a2014 |
=9×
| 1 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
| 1 |
| 2013 |
=1-
| 1 |
| 2013 |
=
| 2012 |
| 2013 |
故答案为:
| 2012 |
| 2013 |
点评:本题主要考查了图形的变化类,解答此题的关键是根据已知的图形中点数的变化推得an=3(n-1)(n≥2).

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线DE与平面A1BC1的夹角为
如图,在正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线DE与平面A1BC1的夹角为