题目内容
 如图,在正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线DE与平面A1BC1的夹角为
如图,在正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线DE与平面A1BC1的夹角为考点:直线与平面所成的角
专题:计算题,空间角
分析:设正方体的棱长为2,直线DE与平面A1BC1的夹角为α,建立如图所示的坐标系,求出平面A1BC1的法向量,利用向量的夹角公式,即可求出直线DE与平面A1BC1的夹角.
解答:
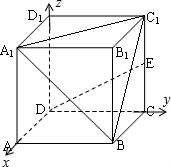 解:设正方体的棱长为2,直线DE与平面A1BC1的夹角为α,建立如图所示的坐标系,则
解:设正方体的棱长为2,直线DE与平面A1BC1的夹角为α,建立如图所示的坐标系,则
D(0,0,0),E(0,2,1),B1(2,2,2,)
∵DB1⊥平面A1BC1,
∴
=(2,2,2)是平面A1BC1的法向量,
∵
=(0,2,1),
∴sinα=
=
,
∴α=arcsin
.
故答案为:arcsin
.
 解:设正方体的棱长为2,直线DE与平面A1BC1的夹角为α,建立如图所示的坐标系,则
解:设正方体的棱长为2,直线DE与平面A1BC1的夹角为α,建立如图所示的坐标系,则D(0,0,0),E(0,2,1),B1(2,2,2,)
∵DB1⊥平面A1BC1,
∴
| DB1 |
∵
| DE |
∴sinα=
| 4+2 | ||||
|
| ||
| 5 |
∴α=arcsin
| ||
| 5 |
故答案为:arcsin
| ||
| 5 |
点评:本题考查直线与平面所成的角,考查向量知识的运用,正确运用向量的夹角公式是关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
边长为1的正三角形ABC中,向量
与
的数量积的值为( )
| AB |
| CB |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
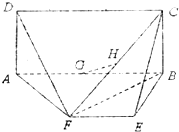 已知矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,AB∥FE,G、H分别为AB、CF的中点,AB=2,AD=EF=1,∠AFB=
已知矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,AB∥FE,G、H分别为AB、CF的中点,AB=2,AD=EF=1,∠AFB=