题目内容
已知a1=1,a2=
,an+1-
an+an-1=0,(n≥2),求an.
| 5 |
| 2 |
| 5 |
| 2 |
考点:数列递推式
专题:计算题,等差数列与等比数列,点列、递归数列与数学归纳法
分析:令an+1-kan=l(an-kan-1),即an+1-(k+l)an+klan-1=0,则有k+l=
,kl=1,解得k=
,l=2,
即有an+1-
an=2(an-
an-1),由等比数列的通项得到bn=2n-1,n>1,即2an-an-1=2n
令2(an+t2n)=an-1+t2n-1,解得t=-
,再由等比数列的通项,即可求得.
| 5 |
| 2 |
| 1 |
| 2 |
即有an+1-
| 1 |
| 2 |
| 1 |
| 2 |
令2(an+t2n)=an-1+t2n-1,解得t=-
| 2 |
| 3 |
解答:
解:∵a1=1,a2=
,an+1-
an+an-1=0,(n≥2),
令an+1-kan=l(an-kan-1),即an+1-(k+l)an+klan-1=0,
则有k+l=
,kl=1,解得k=
,l=2,
即有an+1-
an=2(an-
an-1),
令bn=an-
an-1,则bn+1=2bn,(n>1),
则有bn=b2•2n-2=(a2-
a1)•2n-2=2•2n-2=2n-1,
即有an-
an-1=2n-1,即2an-an-1=2n,
令2(an+t2n)=an-1+t2n-1,解得t=-
,
则an-
•2n=(a2-
•22)•(
)n-2=(
-
)•(
)n-2=-
•(
)n-2,
故an=
.
| 5 |
| 2 |
| 5 |
| 2 |
令an+1-kan=l(an-kan-1),即an+1-(k+l)an+klan-1=0,
则有k+l=
| 5 |
| 2 |
| 1 |
| 2 |
即有an+1-
| 1 |
| 2 |
| 1 |
| 2 |
令bn=an-
| 1 |
| 2 |
则有bn=b2•2n-2=(a2-
| 1 |
| 2 |
即有an-
| 1 |
| 2 |
令2(an+t2n)=an-1+t2n-1,解得t=-
| 2 |
| 3 |
则an-
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
故an=
|
点评:本题考查数列递推式,考查构造等比数列求数列的通项,考查学生的计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知函数f(x)=sin2x+2
cos2x-
,函数g(x)=mcos(2x-
)-2m+3(m>0),若?x1∈[0,
],总?x2∈[0,
],使得g(x1)=f(x2)成立,则实数m的取值范围为( )
| 3 |
| 3 |
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
| A、[1,2] | ||||
B、[1,
| ||||
C、[
| ||||
D、[
|
按照如图的程序图计算,若开始输入的值为3,则最后输出的结果是( )

| A、6 | B、21 |
| C、5050 | D、231 |
不等式组
表示的平面区域面积是( )
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知点A(2,-1,-3),点A关于x轴的对称点为B,则|AB|的值为( )
| A、4 | ||
| B、6 | ||
C、
| ||
D、2
|
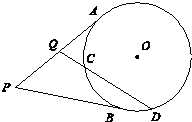 如图,p为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=4,则PB=
如图,p为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=4,则PB=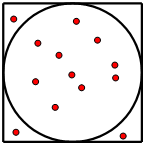 某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在左下图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为35粒,则由此估计出的圆周率π的值为
某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在左下图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为35粒,则由此估计出的圆周率π的值为