题目内容
 如图,ABCD-A1B1C1D1为正方体.
如图,ABCD-A1B1C1D1为正方体.(1)求证:B1D1∥平面BC1D;
(2)求异面直线B1D1与BC1所成角的大小.
考点:直线与平面平行的判定,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)利用直线与平面平行的判定定理,证明仔细与平面平行.
(2)转化异面直线所成角为平面角,求解即可.
(2)转化异面直线所成角为平面角,求解即可.
解答:
解:(1)证明:ABCD-A1B1C1D1为正方体,∴BB1
DD1,四边形BB1D1D是平行四边形,BD?平面平面BC1D,B1D1?平面BC1D,∴B1D1∥平面BC1D.
(2)由(1)可知:B1D1∥BD,异面直线B1D1与BC1所成角就是∠C1BD,
△BC1D是正三角形,所以∠C1BD=60°.
| ∥ |
. |
(2)由(1)可知:B1D1∥BD,异面直线B1D1与BC1所成角就是∠C1BD,
△BC1D是正三角形,所以∠C1BD=60°.
点评:本题考查直线与平面平行的判定定理的应用,异面直线所成角的求法,考查计算能力以及逻辑推理能力.

练习册系列答案
相关题目
圆x2+y2-2x+4y-4=0截直线 x+y-l=0所截得的弦长是( )
| A、2 | ||
B、2
| ||
C、2
| ||
| D、以上都不对 |
已知△ABC中,a=4,b=4
,A=30°,则角B等于( )
| 3 |
| A、30° |
| B、30°或150° |
| C、60°或120° |
| D、60° |
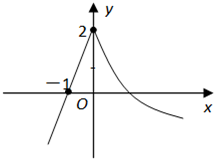 函数f(x)=
函数f(x)=