题目内容
17.已知抛物线y2=2px(p>0)的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,若△FPM为边长是6的等边三角形,则此抛物线的方程为y2=6x.分析 根据题意,设抛物线的准线为l,与x轴交点为N,分析可得FN=p,由抛物线的性质分析可得PM⊥l,进而分析可得△MNF为直角三角形,故PM=2p,又由题意△FPM为边长是6的等边三角形,可得2p=6,即可得抛物线的方程.
解答 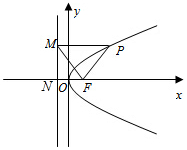 解:根据题意,设抛物线的准线为l,与x轴交点为N,则N(-$\frac{p}{2}$,0),FN=p,
解:根据题意,设抛物线的准线为l,与x轴交点为N,则N(-$\frac{p}{2}$,0),FN=p,
若△FPM为边长是6的等边三角形,即有PF=PM,
则PM⊥l,
又由∠PMF=60°,
则∠PMN=90°-60°=30°,
△MNF为直角三角形,故PM=2p,
又由△FPM为边长是6的等边三角形,即PM=6,
则有2p=6;
即此抛物线的方程为y2=6x;
故答案为:y2=6x.
点评 本题考查抛物线的几何性质,涉及直线与抛物线的位置关系.考查了学生综合把握所学知识和基本的运算能力.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
8.阅读如图所示的程序框图,运行相应的程序,输出的S=( )
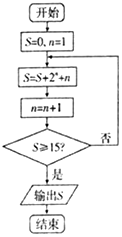

| A. | 40 | B. | 21 | C. | 20 | D. | 18 |
2.已知焦点在x轴上,渐近线方程为$y=±\frac{3}{4}x$的双曲线和曲线$\frac{x^2}{4}+\frac{y^2}{b^2}=1({b>0})$的离心率之积为1,则b的值 为( )
| A. | $\frac{6}{5}$ | B. | 3 | C. | 3或4 | D. | $\frac{6}{5}$或$\frac{10}{3}$ |
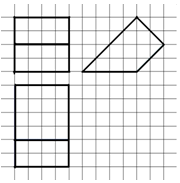 如图,网格上小正方形的边长为$\frac{1}{2}$,粗线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格上小正方形的边长为$\frac{1}{2}$,粗线画出的是某空间几何体的三视图,则该几何体的体积为( )