题目内容
在极坐标系中，圆ρ=2sinθ的圆心到极轴的距离为（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把圆的极坐标方程化为直角坐标方程，求出圆心的直角坐标，可得它到极轴的距离．
解答：
解：圆ρ=2sinθ的直角坐标方程为 x2+（y-1）2=1，它的圆心为（0，1），
故圆心到极轴的距离为1，
故答案为：1．
故圆心到极轴的距离为1，
故答案为：1．
点评：本题主要考查把极坐标方程化为直角坐标方程的方法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若函数f（x）满足f（x）+1=
，当x∈[0，1]时，f（x）=x，若在区间（-1，1]上，方程f（x）-mx-2m=0有两个实数解，则实数m的取值范围是（ ）
| 1 |
| f(x+1) |
A、0＜m≤
| ||
B、0＜m＜
| ||
C、
| ||
D、
|
若函数f（x）=x3-ax2+4在（0，2）内单调递减，则实数a的取值范围为（ ）
| A、[3，+∞） |
| B、{3} |
| C、（-∞，3] |
| D、（0，3） |
如果对x＞0，y＞0，有f（x，y）=（x+4y）（
+
）≥m恒成立，那么实数m的取值范围是（ ）
| 2 |
| x |
| 1 |
| 2y |
| A、（-∞，4] |
| B、（8，+∞） |
| C、（-∞，0） |
| D、（-∞，8] |
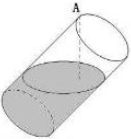一空的圆柱体容器直径小于母线长斜放，将容器斜放，使圆柱的母线与水平面成45°角，现于这种状态下由容器的最高点A处匀速地灌油，如图，则点A到油平面的距离y与灌水时间t的函数图象大致为（ ）A、 |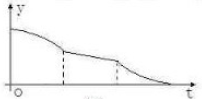
B、 |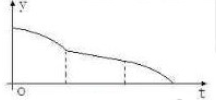
C、 |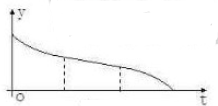
D、 |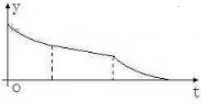
已知集合A={x|-1＜x＜1}，则下列选项中正确的是（ ）
| A、0⊆A | B、{0}∈A |
| C、∅∈A | D、{0}⊆A |
已知圆O：x2+y2=4，直线l：kx-y-k-1=0