题目内容
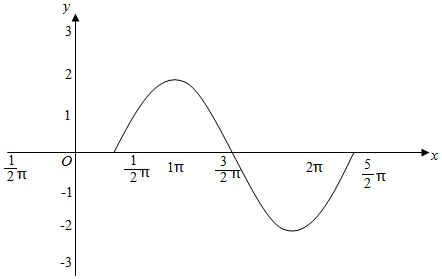
5.已知函数f(x)=2sin(x-$\frac{π}{3}$).(1)用五点法作出函数y=f(x)在区间[$\frac{π}{3}$,$\frac{7π}{3}$]上的大致图象(列表、描点、连线);
(2)若sinα=$\frac{1}{3}$,α∈($\frac{π}{2}$,π),求f(α+$\frac{π}{3}$)+sec2α-tanα的值.

分析 (1)将x-$\frac{π}{3}$的取值,x的取值及f(x)的取值情况列表,利用五点法画图;
(2)由已知求出cosα,根据三角函数公式求值.
解答 解:(1)将x-$\frac{π}{3}$的取值,
x的取值及f(x)的取值情况列表如下:
| x-$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ | $\frac{7π}{3}$ |
| y | 0 | 2 | 0 | -2 | 0 |
(2)sinα=$\frac{1}{3}$,α∈($\frac{π}{2}$,π),所以cosα=-$\frac{2\sqrt{2}}{3}$,
所以f(α+$\frac{π}{3}$)+sec2α-tanα=2sinα+$\frac{1}{co{s}^{2}α}$+$\frac{1}{2\sqrt{2}}$=$\frac{2}{3}+\frac{9}{8}+\frac{\sqrt{2}}{4}=\frac{43+6\sqrt{2}}{24}$.
点评 本题考查了三角函数的五点法画图以及三角函数式的化简求值;明确作图方法以及化简公式是解答的关键.

练习册系列答案
相关题目
16.从一批苹果中,随机抽取65个,其重量(克)的数据分布表如下:
(1)用分层抽样的方法从重量在[80,85)和[95,100)的品种共抽取4个,重量在[80,85)的有几个?
(2)在(1)中抽取4个苹果中任取2个,其重量在[80,85)和[95,100)中各有1个的概率.
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 15 | 30 | 15 |
(2)在(1)中抽取4个苹果中任取2个,其重量在[80,85)和[95,100)中各有1个的概率.
17.下列数列中不是等差数列的为( )
| A. | 6,6,6,6,6 | B. | -2,-1,0,1,2 | C. | 5,8,11,14 | D. | 0,1,3,6,10. |
2.在△ABC中,AB=2,AC=$\sqrt{3}$BC,则当△ABC面积最大值时其周长为( )
| A. | 2$\sqrt{3}$+2 | B. | $\sqrt{3}$+3 | C. | 2$\sqrt{3}$+4 | D. | $\sqrt{3}$+4 |
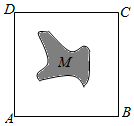 如图,面积为S的正方形ABCD中有一个不规则的图形M,可以用随机模拟方法近似计算M的面积,在正方向ABCD中随机投掷3600个点,若恰好有1200个点落入M中,则M的面积的近似值为$\frac{S}{3}$.
如图,面积为S的正方形ABCD中有一个不规则的图形M,可以用随机模拟方法近似计算M的面积,在正方向ABCD中随机投掷3600个点,若恰好有1200个点落入M中,则M的面积的近似值为$\frac{S}{3}$.