题目内容
6.一个几何体的三视图如图所示,则该几何体的外接球的体积为( )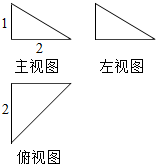
| A. | $\frac{3π}{2}$ | B. | $\frac{9π}{2}$ | C. | $\frac{4π}{3}$ | D. | $\frac{8π}{3}$ |
分析 三视图复原的几何体是长方体的一个角,扩展为长方体,它的外接球的直径就是长方体的对角线的长,求出对角线长,即可求出外接球的体积.
解答 解:三视图复原的几何体是长方体的一个角;把它扩展为长方体,
则长、宽、高分别为1,2,2,
则它的外接球的直径就是长方体的对角线的长,
所以长方体的对角线长为:$\sqrt{1+4+4}$=3,
所以球的半径为:R=$\frac{3}{2}$cm.
这个几何体的外接球的体积是:$\frac{4}{3}$πR3=$\frac{9}{2}$π.
故选:B.
点评 本题是基础题,考查几何体的外接球的问题,空间想象能力,逻辑思维能力,和计算能力,注意本题中三棱锥的外接球与长方体的外接球是同一个球.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
17.直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°则此球的表面积等于( )
| A. | $\frac{52π}{9}$ | B. | 20π | C. | 8π | D. | $\frac{52π}{3}$ |
1.设有直线m、n和平面α、β,则下列说法中正确的是( )
| A. | 若m?α,n?β,α∥β,则m∥n | B. | 若m⊥α,m⊥n,n?β,则α∥β | ||
| C. | 若m∥n,m⊥α,n⊥β,则α⊥β | D. | 若m∥n,m?α,n⊥β,则α⊥β |
11.已知a,b∈R,下列结论成立的是( )
| A. | 若a<b,则ac<bc | B. | 若a<b,c<d,则ac<bd | ||
| C. | 若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a<b,则an<bn(n∈N*,n≥2) |
16.不等式4x2+4bx+1≤0的解集为∅,则( )
| A. | b<1 | B. | b>-1或b<1 | C. | -1<b<1 | D. | b>1或b<-1 |