题目内容
3.已知曲线C1:$\left\{\begin{array}{l}{x=-4+cost}\\{y=3+sint}\end{array}\right.$,(t为参数),曲线C2:$\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{9}$=1.(1)化C1为普通方程,C2为参数方程;并说明它们分别表示什么曲线?
(2)若C1上的点P对应的参数为t=$\frac{π}{2}$,Q为C2上的动点,求PQ中点M到直线C3:x-2y-7=0距离的最小值.
分析 (1)利用参数方程与普通方程的转化方法,可得相应方程及表示的曲线;
(2)求出M的参数坐标,M到C3的距离,利用三角函数知识即可求解.
解答 解:(1)由C1:$\left\{\begin{array}{l}{x=-4+cost}\\{y=3+sint}\end{array}\right.$,消去t得到曲线C1:(x+4)2+(y-3)2=1,
C1表示圆心是(-4,3),半径是1的圆.
曲线C2:$\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{9}$=1表示中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
其参数方程为$\left\{\begin{array}{l}{x=8cosθ}\\{y=3sinθ}\end{array}\right.$(θ为参数)
(2)依题设,当t=$\frac{π}{2}$时,P(-4,4);
且Q(8cos θ,3sin θ),
故M(-2+4cos θ,2+$\frac{3}{2}$sin θ)
又C3为直线x-2y-7=0,
M到C3的距离d=$\frac{\sqrt{5}}{4}$|4cos θ-3sin θ-13|=$\frac{\sqrt{5}}{5}$|5cos(θ+φ)-13|,
从而当cos θ=$\frac{4}{5}$,sin θ=-$\frac{3}{5}$时,其中φ由sin φ=$\frac{3}{5}$,cos φ=$\frac{4}{5}$确定,cos(θ+φ)=1,d取得最小值$\frac{8\sqrt{5}}{5}$.
点评 本题考查参数方程、直角坐标方程的转化,考查参数方程的运用,属于中档题.

练习册系列答案
相关题目
14.设f,g都是由A到A的映射,其对应法则如表(从上到下);
表1 映射f对应法则
表2 映射g的对应法则
则与f[g(1)]相同的是( )
表1 映射f对应法则
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 3 | 4 | 2 | 1 |
| 原像 | 1 | 2 | 3 |
| 像 | 4 | 3 | 1 |
| A. | g[f(3)] | B. | g[f(2)] | C. | g[f(4)] | D. | g[f(1)] |
11.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据完成下面的2×2列联表;
(2)判断性别与休闲方式是否有关系.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
(1)根据以上数据完成下面的2×2列联表;
(2)判断性别与休闲方式是否有关系.
| 休闲方式 性别 | 看电视 | 运动 | 总计 |
| 女 | 43 | 27 | 70 |
| 男 | 21 | 33 | 54 |
| 总计 | 64 | 60 | 124 |
| P(K2≥k ) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
18.某几何体的三视图如图所示,则该几何体的体积为( )
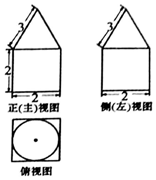

| A. | 4+2$\sqrt{2}$π | B. | 8+2$\sqrt{2}$π | C. | 4+$\frac{2\sqrt{2}}{3}$π | D. | 8+$\frac{2\sqrt{2}}{3}$π |
13.有5位同学排成前后两排拍照,若前排站2人,则甲不站后排两端且甲、乙左右相邻的概率为( )
| A. | $\frac{3}{20}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
