��Ŀ����
12����ƽ��ֱ������ϵxOy�У���б��Ϊ��������$\frac{��}{2}$����ֱ��l�IJ�������Ϊ$\left\{{\begin{array}{l}{x=1+tcos��}\\{y=tsin��}\end{array}}\right.$��tΪ��������������ԭ��Ϊ���㣬��x���������Ϊ���ᣬ����������ϵ������C�ļ����귽���Ǧ�cos2��-4sin��=0����I��д��ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
������֪��P��1��0��������M�ļ�����Ϊ��1��$\frac{��}{2}$����ֱ��l������M��������C�ཻ��A��B���㣬���߶�AB���е�ΪQ����|PQ|��ֵ��
���� ����ֱ��l�IJ���������ȥ����t�������ֱ��l����ͨ���̣�������C�ļ����귽�����������C��ֱ�����귽�̣�
���������M��ֱ������Ϊ��0��1�����Ӷ�ֱ��l����б��Ϊ$��=-\frac{3��}{4}$���ɴ������ֱ��l�IJ������̣�����x2=4y����${t}^{2}-6\sqrt{2}t+2=0$���ɴ�����Τ�ﶨ�����������빫ʽ�����|PQ|��
��� �⣺����ֱ��l�IJ�������Ϊ$\left\{{\begin{array}{l}{x=1+tcos��}\\{y=tsin��}\end{array}}\right.$��tΪ��������
��ֱ��l����ͨ����Ϊy=tan��•��x-1����
������C�ļ����귽���Ǧ�cos2��-4sin��=0���æ�2cos2��-4��sin��=0��
��x2-4y=0��
������C��ֱ�����귽��Ϊx2=4y��
���ߵ�M�ļ�����Ϊ��1��$\frac{��}{2}$�������M��ֱ������Ϊ��0��1����
��tan��=-1��ֱ��l����б��Ϊ$��=-\frac{3��}{4}$��
��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.����tΪ������$��
����x2=4y����${t}^{2}-6\sqrt{2}t+2=0$��
��A��B�����Ӧ�IJ���Ϊt1��t2��
��QΪ�߶�AB���е㣬
���Q��Ӧ�IJ���ֵΪ$\frac{{t}_{1}+{t}_{2}}{2}=\frac{6\sqrt{2}}{2}=3\sqrt{2}$��
��P��1��0������|PQ|=|$\frac{{t}_{1}+{t}_{2}}{2}$|=3$\sqrt{2}$��
���� ���⿼�����ߵ�ֱ�����귽�̵��������ҳ�����Ӧ�ã������������빫ʽ�������е��⣬����ʱҪ�������⣬ע��������̡�ֱ�����귽�̡������귽�̻�����ʽ�ĺ������ã�

 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�| A�� | y=-|x-1| | B�� | y=x2-2x+3 | C�� | y=ln��x+1�� | D�� | y=2${\;}^{-\frac{x}{2}}$ |
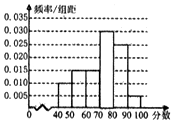 ij��ѧѡȡ20������ͬѧ�μ�2015��Ӣ��Ӧ��֪ʶ�����������ǵijɼ����ٷ��ƣ�����Ϊ�������ֳ�6��õ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�����۲�ͼ���е���Ϣ���ش��������⣮
ij��ѧѡȡ20������ͬѧ�μ�2015��Ӣ��Ӧ��֪ʶ�����������ǵijɼ����ٷ��ƣ�����Ϊ�������ֳ�6��õ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�����۲�ͼ���е���Ϣ���ش��������⣮