题目内容
11.已知数列{an}中,a1=1,a2=3,an+2+an=an+1,则a2014=( )| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
分析 由条件an+2+an=an+1,可得an+2=an+1-an,得到an+6=an,从而确定数列是周期数列,利用数列的周期性即可求解.
解答 解:∵an+2+an=an+1,∴an+2=an+1-an.
∴an+3=an+2_an+1=an+1-an-an+1=-an,即an+6=-an+3=an,
即数列{an}是周期为6的周期数列.
∴a2014=a335×6+4=a4,
∵a1=1,a2=3,an+2=an+1-an,
∴a3=a2-a1=3-1=2,
a4=a3-a2=2-3=-1.
故a2014=a4=-1.
故选:B.
点评 本题主要考查数列项的计算,利用条件求出数列是周期数列是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知集合A={x|x2-4x+3<0},B={|x|$\frac{x-4}{2-x}$≥0},则A∩B=( )
| A. | [2,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |
2.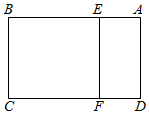 如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
 如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )| A. | 68% | B. | 70% | C. | 72% | D. | 75% |
19.当a>0,a≠1时,函数f(x)=loga(x-1)+1的图象恒过定点A,若点A在直线mx-y+n=0上,则4m+2n的最小值是( )
| A. | 4 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
6.设函数f(x)=$\left\{\begin{array}{l}{log_3}x,0<x≤9\\ f(x-4),x>9\end{array}$则$f(13)+2f(\frac{1}{3})$的值为( )
| A. | 1 | B. | 0 | C. | -2 | D. | 2 |
3.抛物线y2=12x上与焦点的距离等于9的点的坐标( )
| A. | $(6,±6\sqrt{2})$ | B. | $(6\sqrt{2},±6)$ | C. | $(12,±6\sqrt{2})$ | D. | $(6\sqrt{2},±12)$ |