题目内容
不等式|x-1|+|x+2|≤a的解集非空，则实数a的取值范围是（ ）
| A、a＞3 | B、a≥3 |
| C、a≤4 | D、a≥4 |
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：令g（x）=|x-1|+|x+2|，由绝对值的几何意义可知g（x）=|x-1|+|x+2|≥3，从而可得实数a的取值范围．
解答：
解：令g（x）=|x-1|+|x+2|，
由绝对值的几何意义得：g（x）=|x-1|+|x+2|≥|1-x+x+2|=3，
又不等式|x-1|+|x+2|≤a在R上的解集非空，
∴a≥g（x）min=3．
故选：B．
由绝对值的几何意义得：g（x）=|x-1|+|x+2|≥|1-x+x+2|=3，
又不等式|x-1|+|x+2|≤a在R上的解集非空，
∴a≥g（x）min=3．
故选：B．
点评：本题考查绝对值不等式，由绝对值的几何意义得到g（x）=|x-1|+|x+2|≥3是解答本题的关键．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
从2010名学生中选50人组成参观团，先用简单随机抽样方法剔除10人，再将其余2000人按系统抽样方法选取，则每人入选的概率（ ）
| A、不全相等 | ||
| B、B均不相等 | ||
C、都是
| ||
D、都是
|
已知复数z=a2-1+（a+1）i（a∈R）为纯虚数，则
为（ ）
. |
| z |
| A、0 | B、2i |
| C、-2i | D、-1-2i |
设全集U=R，A={x|x（x-2）＜0}，B={x|y=ln（1-x）＜0}，则图中阴影部分表示的集合为（ ）
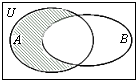
| A、{x|0＜x≤1} |
| B、{x|1≤x＜2} |
| C、{x|x≥1} |
| D、{x|x≤1} |
f（x）=lnx+x2-3x的极大值点是（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
函数y=（
）x+2+1（a＞0，a≠1）图象必经过点（ ）
| 1 |
| a |
| A、（-1，1） |
| B、（-1，2） |
| C、（-2，1） |
| D、（-2，2） |
国庆节放假，甲、乙、丙去北京旅游的概率分别是
，
，
．假定三人的行动相互之间没有影响，那么这段时间内至少有1人去北京旅游的概率为（ ）
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|