题目内容
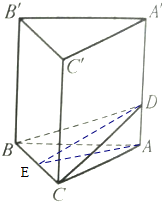
如图，正三棱柱的底面边长是4cm，过BC的一个平面交侧棱AA'于D，若AD=2cm，求截面△BCD的面积．
考点：平行投影及平行投影作图法
专题：空间位置关系与距离
分析：根据三角形的面积公式即可得到结论．
解答：
解：取BC的中点E，连接AE，DE，
则AE，DE分别是△ABC，△BCD的高，
∵正三角形ABC的边长为4，
∴AE=2
，
∵AD=2，∴DE=
=
=
=
=4，
则截面△BCD的面积S=
BC•DE=
×4×4=8．
解：取BC的中点E，连接AE，DE，则AE，DE分别是△ABC，△BCD的高，
∵正三角形ABC的边长为4，
∴AE=2
| 3 |
∵AD=2，∴DE=
| AE2+AD2 |
22+(2
|
| 4+12 |
| 16 |
则截面△BCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
点评：本题主要考查三角形的面积的计算，根据条件求出三角形的高是解决本题的关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
已知f（x）=
x2+2xf′（2014）+2014lnx，则f′（2014）=（ ）
| 1 |
| 2 |
| A、2015 | B、-2015 |
| C、2014 | D、-2014 |
如图，某工厂生产的一种无盖纸筒为圆锥形，现一客户订制该圆锥纸筒，并要求该圆锥纸筒的容积为π立方分米．设圆锥纸筒底面半径为r分米，高为h分米．某三棱锥的三视图如图所示，则该三棱锥的全面积是（ ）
A、4+2
| ||
| B、8 | ||
C、4+2
| ||
D、4
|