题目内容
已知抛物线y2=8x与双曲线
-y2=1的一个交点为M,F为抛物线的焦点,若|MF|=5,则该双曲线的渐近线方程为( )
| x2 |
| a2 |
| A、5x±3y=0 |
| B、3x±5y=0 |
| C、4x±5y=0 |
| D、5x±4y=0 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求得抛物线的焦点和准线方程,设M(m,n),则由抛物线的定义可得m=3,进而得到M的坐标,代入双曲线的方程,可得a,再由渐近线方程即可得到所求.
解答:
解:抛物线y2=8x的焦点F(2,0),准线方程为x=-2,
设M(m,n),则由抛物线的定义可得
|MF|=m+2=5,解得m=3,
由n2=24,可得n=±2
.
将M(3,±2
)代入双曲线
-y2=1,
可得
-24=1,解得a=
,
即有双曲线的渐近线方程为y=±
x.
即为5x±3y=0.
故选A.
设M(m,n),则由抛物线的定义可得
|MF|=m+2=5,解得m=3,
由n2=24,可得n=±2
| 6 |
将M(3,±2
| 6 |
| x2 |
| a2 |
可得
| 9 |
| a2 |
| 3 |
| 5 |
即有双曲线的渐近线方程为y=±
| 5 |
| 3 |
即为5x±3y=0.
故选A.
点评:本题考查抛物线和双曲线的定义、方程和性质,主要考查抛物线的定义和双曲线的渐近线方程,考查运算能力,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知∠ABC=90°,PA⊥平面ABC,若PA=AB=BC=1,则四面体PABC的外接球(顶点都在球面上)的表面积为( )
| A、π | ||
B、
| ||
| C、2π | ||
| D、3π |
双曲线
-
=1(a>0)的离心率为( )
| x2 |
| a2 |
| y2 |
| 4a2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
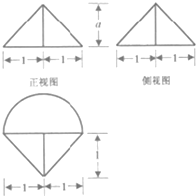 一个几何体的三视图如图,其中正视图和侧视图是相同的等腰三角形,俯视图由半圆和一等腰三角形组成.则这个几何体可以看成是由
一个几何体的三视图如图,其中正视图和侧视图是相同的等腰三角形,俯视图由半圆和一等腰三角形组成.则这个几何体可以看成是由