题目内容
在△ABC中,内角A、B、C的对边分别是a、b、c,且a2=b2+c2+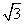 bc.
bc.
(1)求A;
(2)设a=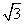 ,S为△ABC的面积,求S+3cos Bcos C的最大值,并指出此时B的值.
,S为△ABC的面积,求S+3cos Bcos C的最大值,并指出此时B的值.
解析:(1)由余弦定理得
cos A= =
= =-
=- .
.
又因0<A<π,所以A= .
.
(2)由(1)得sin A= ,
,
又由正弦定理及a=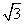 得
得
S= bcsin A=
bcsin A= ·
· ·asin C=3sin Bsin C,
·asin C=3sin Bsin C,
因此,S+3cos Bcos C=3(sin Bsin C+cos Bcos C)
=3cos(B-C).
所以,当B=C,即B= 时,S+3cos Bcos C取得最大值3.
时,S+3cos Bcos C取得最大值3.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目

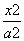 +
+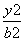 =1(a>b>0)上一点P,F1、F2为椭圆
=1(a>b>0)上一点P,F1、F2为椭圆 的焦点,若∠F1PF2=θ,则△PF1F2的面积等于________.
的焦点,若∠F1PF2=θ,则△PF1F2的面积等于________. 表示的直线是( )
表示的直线是( )
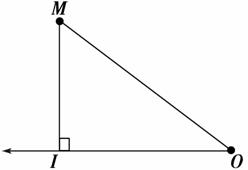
 B.
B. C.3 D.
C.3 D.
 已知函数f(x)=Atan(ωx+φ)ω>0,|φ|<
已知函数f(x)=Atan(ωx+φ)ω>0,|φ|< ,y=f(x)的部分图象如下图所示,则f
,y=f(x)的部分图象如下图所示,则f =( )
=( )
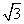 B.
B. D.2-
D.2- ,现有下列结论:
,现有下列结论: 对称;
对称; 对称;
对称; 个单位长度,得到一个偶函数的图象;
个单位长度,得到一个偶函数的图象; 上为增函数.
上为增函数. ,求向量a与c的夹角θ;
,求向量a与c的夹角θ; ,函数f(x)=λa·b的最大值为
,函数f(x)=λa·b的最大值为 ,求实数λ的值.
,求实数λ的值. 函数值的符号判断错误的是( )
函数值的符号判断错误的是( ) 80°>0
80°>0