题目内容
.(本小题满分14分)已知椭圆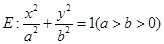 上的点
上的点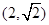 到两个焦点的距离之和为
到两个焦点的距离之和为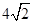 。
。
(Ⅰ)求椭圆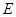 的方程;
的方程;
(Ⅱ)若直线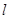 与椭圆
与椭圆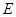 交于两点
交于两点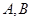 ,且
,且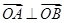 (
(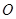 为坐标原点),求
为坐标原点),求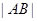 的最大值和最小值。
的最大值和最小值。
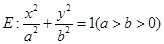 上的点
上的点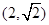 到两个焦点的距离之和为
到两个焦点的距离之和为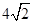 。
。(Ⅰ)求椭圆
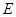 的方程;
的方程;(Ⅱ)若直线
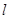 与椭圆
与椭圆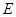 交于两点
交于两点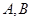 ,且
,且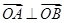 (
(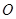 为坐标原点),求
为坐标原点),求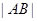 的最大值和最小值。
的最大值和最小值。解:(Ⅰ) ∵
 ,∴
,∴ ,故椭圆
,故椭圆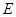 的方程
的方程 (2分).
(2分).(Ⅱ)设直线
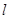 的方程为
的方程为 ,解方程组
,解方程组 得
得 ,即
,即 ,则△=
,则△=
∵
 (4分),
(4分),∴

∴


 ,即
,即 ,∴
,∴ (6分)
(6分)解法一:∵

 (8分)
(8分)1、当
 时
时 ,∵
,∵ ,∴
,∴ ,
,∴
 ,∴
,∴ ,当且仅当
,当且仅当 时取”=”;
时取”=”;2、当
 时,
时, (10分)
(10分)3、当AB斜率不存在时, 两交点为
 或
或 ,
, (11分)
(11分)综上,当
 时,
时, ;当
;当 或
或 不存在时,
不存在时, (14分)
(14分)略

练习册系列答案
相关题目
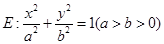 的左右焦点为
的左右焦点为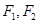 ,过点
,过点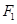 且斜率为正数的直线
且斜率为正数的直线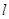 交椭圆
交椭圆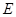 于
于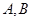 两点,且
两点,且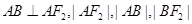 成等差数列。
成等差数列。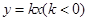 与椭圆
与椭圆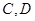 两点,求使四边形
两点,求使四边形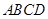 的面积最大时的
的面积最大时的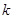 值。
值。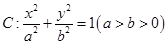 的左、右焦点分别为
的左、右焦点分别为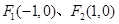 ,且经过定点
,且经过定点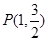 ,
,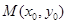 为椭圆
为椭圆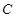 上的动点,以点
上的动点,以点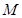 为圆心,
为圆心,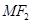 为半径作圆
为半径作圆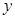 轴有两个不同交点,求点
轴有两个不同交点,求点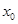 的取值范围;
的取值范围;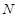 ,使得圆
,使得圆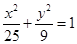 上的点
上的点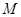 到焦点
到焦点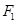 的距离为2,
的距离为2,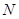 为
为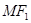 的中点,则
的中点,则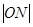 (
(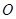 为坐标原点)的值为
为坐标原点)的值为 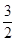
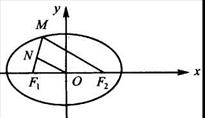
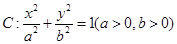 的一个焦点为
的一个焦点为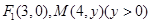 为椭圆上一点,
为椭圆上一点,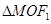 的面积为
的面积为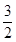
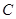 的方程;
的方程;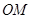 的直线
的直线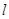 ,使得直线
,使得直线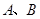 两点,且以线段
两点,且以线段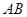 为有经的圆恰好经过原点?若存在,求出
为有经的圆恰好经过原点?若存在,求出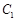 :
: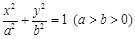 的离心率为
的离心率为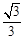 ,直线
,直线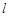 :
: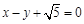 与椭圆
与椭圆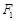 ,右焦点为
,右焦点为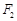 ,直线
,直线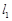 过点
过点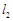 垂直于直线
垂直于直线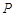 ,线段
,线段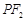 的垂直平分线交
的垂直平分线交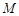 ,求点
,求点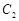 的方程.
的方程.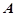 和
和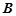 ,且
,且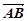 与
与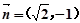 共线.
共线.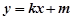 与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
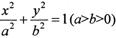 的左、右焦点分别为
的左、右焦点分别为 ,离心率
,离心率 ,A为右顶点,K为右准线与X轴的交点,且
,A为右顶点,K为右准线与X轴的交点,且 .
.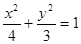 的焦距等于
的焦距等于