题目内容
(.(本小题满分12分)
如图,焦距为2的椭圆E的两个顶点分别为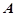 和
和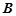 ,且
,且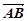 与
与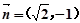 共线.
共线.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线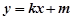 与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
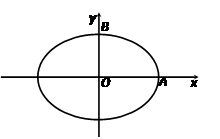
如图,焦距为2的椭圆E的两个顶点分别为
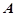 和
和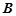 ,且
,且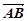 与
与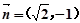 共线.
共线.(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线
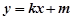 与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.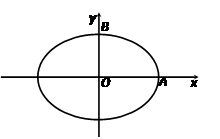
解:(Ⅰ)设椭圆E的标准方程为 ,由已知得
,由已知得
 ,∴
,∴ ,∵
,∵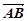 与
与 共线,∴
共线,∴ ,又
,又 (3分)
(3分)
∴ , ∴椭圆E的标准方程为
, ∴椭圆E的标准方程为 (5分)
(5分)
(Ⅱ)设 ,把直线方程
,把直线方程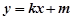 代入椭圆方程
代入椭圆方程 ,
,
消去y,得, ,
,
∴ ,
,  (7分)
(7分)
 (*) (8分)
(*) (8分)
∵原点O总在以PQ为直径的圆内,∴ ,即
,即 (9分)
(9分)
又
由 得
得 ,依题意
,依题意 且满足(*) (11分)
且满足(*) (11分)
故实数m的取值范围是 (12分)
(12分)
 ,由已知得
,由已知得
 ,∴
,∴ ,∵
,∵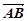 与
与 共线,∴
共线,∴ ,又
,又 (3分)
(3分)∴
 , ∴椭圆E的标准方程为
, ∴椭圆E的标准方程为 (5分)
(5分)(Ⅱ)设
 ,把直线方程
,把直线方程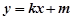 代入椭圆方程
代入椭圆方程 ,
,消去y,得,
 ,
,∴
 ,
,  (7分)
(7分) (*) (8分)
(*) (8分)∵原点O总在以PQ为直径的圆内,∴
 ,即
,即 (9分)
(9分)又

由
 得
得 ,依题意
,依题意 且满足(*) (11分)
且满足(*) (11分)故实数m的取值范围是
 (12分)
(12分)略

练习册系列答案
相关题目
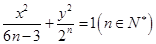 ,若椭圆的焦距为
,若椭圆的焦距为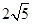 ,则
,则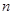 的取值集合为 。
的取值集合为 。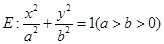 上的点
上的点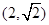 到两个焦点的距离之和为
到两个焦点的距离之和为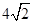 。
。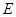 的方程;
的方程;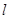 与椭圆
与椭圆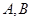 ,且
,且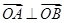 (
(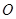 为坐标原点),求
为坐标原点),求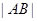 的最大值和最小值。
的最大值和最小值。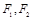 是椭圆
是椭圆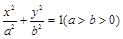 的两个焦点, 若存在点P为椭圆上一点, 使得
的两个焦点, 若存在点P为椭圆上一点, 使得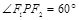 , 则椭圆离心率
, 则椭圆离心率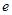 的取值范围是
的取值范围是



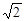 倍,则椭圆的离心率等于( )
倍,则椭圆的离心率等于( ) ;
; ;
; ;
; ;
;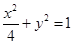 的焦点为
的焦点为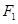 、
、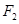 ,在长轴
,在长轴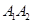 上任取一点
上任取一点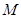 ,过
,过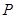 ,则使得
,则使得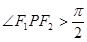 的
的




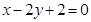 经过椭圆
经过椭圆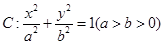 的左顶点
的左顶点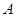 和上顶点
和上顶点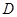 ,椭圆
,椭圆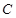 的右顶点为
的右顶点为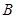 ,点
,点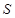 是椭圆
是椭圆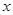 轴上方的动点,直线
轴上方的动点,直线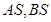 与直线
与直线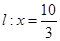 分别交于
分别交于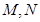 两点.
两点.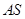 与直线
与直线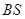 斜率
斜率 的乘积为定值;
的乘积为定值;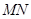 的长度的最小值.
的长度的最小值.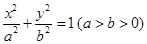 的长轴长为
的长轴长为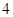 ,且点
,且点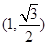 在椭圆上.
在椭圆上.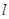 交椭圆于
交椭圆于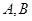 两点,若以
两点,若以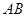 为直径的圆过原点,
为直径的圆过原点,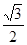 ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为 __
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为 __