题目内容
在△ABC中，已知A=120°，a=14，b+c=16，则△ABC的面积为 ．
考点：余弦定理,正弦定理
专题：解三角形
分析：利用余弦定理可得bc，再利用三角形的面积计算公式即可得出．
解答：
解：由余弦定理可得：a2=b2+c2-2bccosA，
∴142=（b+c）2-2bc-2bccos120°，
∴142=162-2bc+bc，
解得bc=60．
∴△ABC的面积S=
bcsinA=
×60×sin120°=15
．
故答案为：15
．
∴142=（b+c）2-2bc-2bccos120°，
∴142=162-2bc+bc，
解得bc=60．
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
故答案为：15
| 3 |
点评：本题考查了余弦定理可、三角形的面积计算公式，考查了计算能力，属于基础题．
练习册系列答案
相关题目
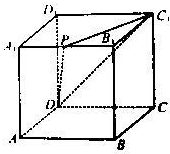如图所示，若点P为正方体AC1的棱A1B1的中点，求截面PC1D和AA1B1B所成的锐二面角的余弦值．
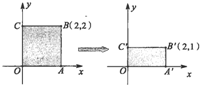已知矩阵M=已知抛物线的焦点F（a，0）（a＜0），则抛物线的标准方程是（ ）
| A、y2=2ax |
| B、y2=4ax |
| C、y2=-2ax |
| D、y2=-4ax |