题目内容
已知O为空间直角坐标系的原点，以下能使向量
，
，
共面的三点A，B，C的坐标是（ ）
| OA |
| OB |
| OC |
| A、A（1，0，0），B（0，1，0），C（0，0，1） |
| B、A（1，2，3），B（3，0，2），C（4，2，5） |
| C、A（1，1，0），B（1，0，1），C（0，1，1） |
| D、A（1，1，1），B（1，1，0），C（1，0，1） |
考点：共线向量与共面向量
专题：空间向量及应用
分析：如果向量
，
，
共面，那么它们可以线性表示，由此对选项分析，找出正确答案．
| OA |
| OB |
| OC |
解答：
解：由题意选项A，C，D的对应向量不能线性表示，
对于选项B，
向量
=（1，2，3），
=（3，0，2），
=（4，2，5），
所以向量
+
=（1，2，3）+（3，0，2）=（4，2，5）=
；
所以向量
，
，
共面．
故选：B．
对于选项B，
向量
| OA |
| OB |
| OC |
所以向量
| OA |
| OB |
| OC |
所以向量
| OA |
| OB |
| OC |
故选：B．
点评：本题考查了空间向量共面的判断，利用共面向量基本定理解答，属于基础题．
练习册系列答案
走进文言文系列答案
相关题目
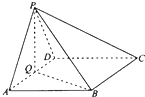如图，四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q是AD的中点．