题目内容
下列四个命题:
①若0>a>b,则
<
;
②x>0,x+
的最小值为3;
③椭圆
+
=1比椭圆
+
=1更接近于圆;
④设A,B为平面内两个定点,若有|PA|+|PB|=2,则动点P的轨迹是椭圆;
其中真命题的序号为 .(写出所有真命题的序号)
①若0>a>b,则
| 1 |
| a |
| 1 |
| b |
②x>0,x+
| 1 |
| x-1 |
③椭圆
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 3 |
| y2 |
| 2 |
④设A,B为平面内两个定点,若有|PA|+|PB|=2,则动点P的轨迹是椭圆;
其中真命题的序号为
考点:命题的真假判断与应用
专题:常规题型,不等式的解法及应用,圆锥曲线的定义、性质与方程,简易逻辑
分析:①利用不等式的性质可得,若0>a>b,则
<
;
②注意基本不等式成立的条件,举反例x=
时;
③求两个椭圆的离心率,由离心率越小越接近于圆可知,椭圆
+
=1比椭圆
+
=1更接近于圆;
④由椭圆的定义可知,若|AB|=2,则动点P的轨迹是线段AB;
| 1 |
| a |
| 1 |
| b |
②注意基本不等式成立的条件,举反例x=
| 1 |
| 2 |
③求两个椭圆的离心率,由离心率越小越接近于圆可知,椭圆
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 3 |
| y2 |
| 2 |
④由椭圆的定义可知,若|AB|=2,则动点P的轨迹是线段AB;
解答:
解:①∵0>a>b,
∴
>0,
不等式两边同乘
可得,
∴
<
;
②若x=
,则x+
=-
,故错误;
③∵椭圆
+
=1的离心率e=
,椭圆
+
=1的离心率e=
,
又∵
>
,
∴椭圆
+
=1比椭圆
+
=1更接近于圆;
④若|AB|=2,则动点P的轨迹是线段AB;
故答案为:①③.
∴
| 1 |
| ab |
不等式两边同乘
| 1 |
| ab |
∴
| 1 |
| a |
| 1 |
| b |
②若x=
| 1 |
| 2 |
| 1 |
| x-1 |
| 3 |
| 2 |
③∵椭圆
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 2 |
| x2 |
| 3 |
| y2 |
| 2 |
| ||
| 3 |
又∵
| ||
| 3 |
| 1 |
| 2 |
∴椭圆
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 3 |
| y2 |
| 2 |
④若|AB|=2,则动点P的轨迹是线段AB;
故答案为:①③.
点评:本题考查了不等式的性质与基本不等式的应用,同时考查了椭圆的性质与定义及命题的真假性的判断,属于中档题.

练习册系列答案
相关题目
设a=90.9,b=270.48,c=(
)-1.5,则a,b,c的大小顺序为( )
| 1 |
| 3 |
| A、a>b>c |
| B、a>c>b |
| C、b>a>c |
| D、c>a>b |
已知O为空间直角坐标系的原点,以下能使向量
,
,
共面的三点A,B,C的坐标是( )
| OA |
| OB |
| OC |
| A、A(1,0,0),B(0,1,0),C(0,0,1) |
| B、A(1,2,3),B(3,0,2),C(4,2,5) |
| C、A(1,1,0),B(1,0,1),C(0,1,1) |
| D、A(1,1,1),B(1,1,0),C(1,0,1) |
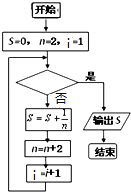 如图所示给出的是计算
如图所示给出的是计算