题目内容
16．已知sin（x+$\frac{π}{2}$）=$\frac{1}{3}$，则cos2x=（ ）| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | -$\frac{7}{9}$ | D． | $\frac{7}{9}$ |
分析 由条件利用诱导公式、二倍角的余弦公式，化简所给式子的值，可得结果．
解答 解：∵sin（x+$\frac{π}{2}$）=cosx=$\frac{1}{3}$，则cos2x=2cos2x-1=-$\frac{7}{9}$，
故选：C．
点评 本题主要考查诱导公式、二倍角的余弦公式的应用，属于基础题．
练习册系列答案
相关题目
7．已知动圆过定点A（3，0），且与圆（x+3）2+y2=64相切，则动圆的圆心P的轨迹是（ ）
| A． | 圆 | B． | 椭圆 | C． | 抛物线 | D． | 双曲线 |
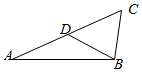如图，在三角形ABC中，AB=x，BC=1，O是AC的中点，∠BOC=45°，记点C到AB的距离为h（x）．
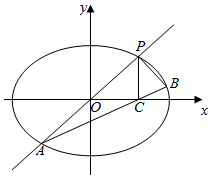已知椭圆w：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）过点（0，$\sqrt{2}$），椭圆w上任意一点到两焦点的距离之和为4．
4．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{1}{2}$x，则双曲线的离心率为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{5}{4}$ | D． | $\frac{\sqrt{5}}{2}$ |