题目内容
6.设函数f(x)=1-$\sqrt{3}$cos2x-2sin2($\frac{π}{4}$-x),x∈R.求:(Ⅰ)f(x)的最小正周期;
(Ⅱ)f(x)在闭区间[-$\frac{π}{3}$,$\frac{π}{2}$]上的最大值与最小值.
分析 (1)由二倍角公式两角和的正弦公式将f(x)=2sin(2x-$\frac{π}{3}$),再求f(x)的最小正周期;
(2)先求得2x-$\frac{π}{3}$的取值范围,再由正弦函数图象求得最大值和最小值.
解答 解:(Ⅰ)f(x)=1-$\sqrt{3}$cos2x-2sin2($\frac{π}{4}$-x),x∈R.
=cos[2($\frac{π}{4}$-x)]-$\sqrt{3}$cos2x,
=cos($\frac{π}{2}$-2x)-$\sqrt{3}$cos2x,
=sin2x-$\sqrt{3}$cos2x,
=2sin(2x-$\frac{π}{3}$),
f(x)的最小正周期T=$\frac{2π}{ω}$=π,
∴f(x)的最小正周期T=π;
(Ⅱ)x∈[-$\frac{π}{3}$,$\frac{π}{2}$],2x-$\frac{π}{3}$∈[-π,$\frac{2π}{3}$],
由正弦函数图象可知,f(x)的最大值为2,最小值为-2.
∴f(x)的最大值为2,最小值为-2.
点评 本题考查三角恒等变换与正弦函数图象相结合,化简过程简单,属于中档题.

练习册系列答案
相关题目
14.曲线$\left\{\begin{array}{l}{x=|sinθ|}\\{y=cosθ}\end{array}\right.$(θ为参数)的方程等价于( )
| A. | x=$\sqrt{1-{y}^{2}}$ | B. | y=$\sqrt{1-{x}^{2}}$ | C. | y=±$\sqrt{1-{x}^{2}}$ | D. | x2+y2=1 |
1.袋中有大小完全相同的2个红球和3个黑球,不放回地摸出两球,设“第一次摸出红球”为事件A,“摸得的两球同色”为事件B,则概率P(B|A)为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
11.记等式1•n+2•(n-1)+3•(n-2)+…+n•1=$\frac{1}{6}$n(n+1)(n+2)左边的式子为f(n),用数学归纳法证明该等式的第二步归纳递推时,即当n从k变为k+1时,等式左边的改变量f(k+1)-f(k)=( )
| A. | k+1 | B. | 1•(k+1)+(k+1)•1 | C. | 1+2+3+…+k | D. | 1+2+3+…+k+(k+1) |
16.已知sin(x+$\frac{π}{2}$)=$\frac{1}{3}$,则cos2x=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
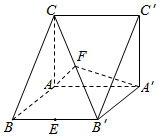 在三棱ABC-A′B′C′中,侧棱AA′⊥底面ABC,AC⊥AB,AB=2,AC=AA′=3,
在三棱ABC-A′B′C′中,侧棱AA′⊥底面ABC,AC⊥AB,AB=2,AC=AA′=3,