题目内容
1.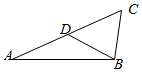 如图,在三角形ABC中,AB=x,BC=1,O是AC的中点,∠BOC=45°,记点C到AB的距离为h(x).
如图,在三角形ABC中,AB=x,BC=1,O是AC的中点,∠BOC=45°,记点C到AB的距离为h(x).(1)求h(x)的表达式,并注明x的取值范围;
(2)求h(x)的最大值.
分析 (1)通过设OB=a,OA=OC=b,利用根据余弦定理计算可知4abcos45°=x2-1,通过三角形面积公式计算可知h(x)=$\frac{{x}^{2}-1}{2x}$,利用基本不等式计算可知1<x≤$\sqrt{2}$+1;
(2)通过(1)求导可知h(x)=$\frac{{x}^{2}-1}{2x}$在区间(1,$\sqrt{2}$+1]上单调递增,进而计算可得结论.
解答 解:(1)作CE垂直AB,OD垂直AB,
设OB=a,OA=OC=b,由根据余弦定理有:
a2+b2-2abcos45°=1,a2+b2+2abcos45°=x2,
两式相减得到:4abcos45°=x2-1,
∵S△AOB=S△COB=$\frac{1}{2}$S△ABC,
∴$\frac{1}{2}$absin45°=$\frac{1}{2}$•$\frac{x}{2}$•h(x),即h(x)=$\frac{2}{x}$absin45°,
消去a、b后得到:h(x)=$\frac{{x}^{2}-1}{2x}$,
一方面显然x2-1>0,即x>1,
另一方面,a2+b2≥2ab,即$\frac{{x}^{2}+1}{2}$≥2•$\frac{{x}^{2}-1}{2\sqrt{2}}$,
综上所述,1<x≤$\sqrt{2}$+1;
(2)由(1)可知,h′(x)=$\frac{{x}^{2}-1}{2x}$=$\frac{2x•2x-2({x}^{2}-1)}{(2x)^{2}}$=$\frac{1+2{x}^{2}}{4{x}^{2}}$>0,
∴h(x)=$\frac{{x}^{2}-1}{2x}$在区间(1,$\sqrt{2}$+1]上单调递增,
∴hmax(x)=$\frac{(\sqrt{2}+1)^{2}-1}{2(\sqrt{2}+1)}$=1.
点评 本题考查函数的最值及其几何意义,涉及考查余弦定理的运用、三角形面积、基本不等式等基础知识,注意解题方法的积累,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | k+1 | B. | 1•(k+1)+(k+1)•1 | C. | 1+2+3+…+k | D. | 1+2+3+…+k+(k+1) |
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 11 | 10 | 15 | A4 | A5 |
| B型数量(台) | 9 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
(2)为跟踪调查空调的使用情况,根据销售记录,从前三周售出的所有空调中随机抽取一台,求抽到的空调不是B型且不是第一周售出空调的概率;
(3)根据C型空调前三周的销售情况,预估C型空调五周的平均周销售量为10台,当C型空调周销售量的方差最小时,求C4,C5的值.
(注:方差s2=$\frac{1}{n}$[(x${\;}_{1}-\overline{x}$)2+(x${\;}_{2}-\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为x1,x2,…,xn的平均数)
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
| A. | 0 | B. | -240 | C. | -480 | D. | 960 |

 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM. 如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.
如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.