题目内容
10．设变量x，y满足约束条件$\left\{\begin{array}{l}{2x+y≥0}\\{x+2y-2≥0}\\{x≤0}\\{y≤3}\end{array}\right.$，则目标函数z=x+y的最大值为（ ）| A． | $\frac{2}{3}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 3 |
分析 画出约束条件的可行域，利用目标函数的最优解求解即可．
解答 
解：变量x，y满足约束条件$\left\{\begin{array}{l}{2x+y≥0}\\{x+2y-2≥0}\\{x≤0}\\{y≤3}\end{array}\right.$的可行域如图：
目标函数z=x+y结果可行域的A点时，目标函数取得最大值，
由$\left\{\begin{array}{l}{y=3}\\{x=0}\end{array}\right.$可得A（0，3），目标函数z=x+y的最大值为：3．
故选：D．
点评 本题考查线性规划的简单应用，考查计算能力以及数形结合思想的应用．
练习册系列答案
全优点练单元计划系列答案
相关题目
16．甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（ ）
| A． | 乙可以知道四人的成绩 | B． | 丁可以知道四人的成绩 | ||
| C． | 乙、丁可以知道对方的成绩 | D． | 乙、丁可以知道自己的成绩 |
18．已知当x∈[0，1]时，函数y=（mx-1）2 的图象与y=$\sqrt{x}$+m的图象有且只有一个交点，则正实数m的取值范围是（ ）
| A． | （0，1]∪[2$\sqrt{3}$，+∞） | B． | （0，1]∪[3，+∞） | C． | （0，$\sqrt{2}$）∪[2$\sqrt{3}$，+∞） | D． | （0，$\sqrt{2}$]∪[3，+∞） |
已知{xn}是各项均为正数的等比数列，且x1+x2=3，x3-x2=2．
15．设函数f（x）=2sin（ωx+φ），x∈R，其中ω＞0，|φ|＜π．若f（$\frac{5π}{8}$）=2，f（$\frac{11π}{8}$）=0，且f（x）的最小正周期大于2π，则（ ）
| A． | ω=$\frac{2}{3}$，φ=$\frac{π}{12}$ | B． | ω=$\frac{2}{3}$，φ=-$\frac{11π}{12}$ | C． | ω=$\frac{1}{3}$，φ=-$\frac{11π}{24}$ | D． | ω=$\frac{1}{3}$，φ=$\frac{7π}{24}$ |
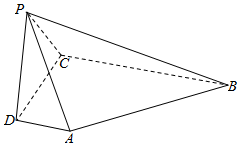如图，在四棱锥P-ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．