Question

5．已知{x_n}是各项均为正数的等比数列，且x₁+x₂=3，x₃-x₂=2．
（Ⅰ）求数列{x_n}的通项公式；
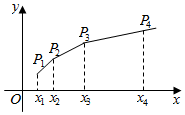
（Ⅱ）如图，在平面直角坐标系xOy中，依次连接点P₁（x₁，1），P₂（x₂，2）…P_n+1（x_n+1，n+1）得到折线P₁ P₂…P_n+1，求由该折线与直线y=0，x=x₁，x=x_n+1所围成的区域的面积T_n．

Answer 1

分析 （I）列方程组求出首项和公比即可得出通项公式；
（II）从各点向x轴作垂线，求出梯形的面积的通项公式，利用错位相减法求和即可．

解答 解：（I）设数列{x_n}的公比为q，则q＞0，
由题意得$\left\{\begin{array}{l}{{x}_{1}+{x}_{1}q=3}\\{{x}_{1}{q}^{2}-{x}_{1}q=2}\end{array}\right.$，
两式相比得：$\frac{1+q}{{q}^{2}-q}=\frac{3}{2}$，解得q=2或q=-$\frac{1}{3}$（舍），
∴x₁=1，
∴x_n=2^n-1．
（II）过P₁，P₂，P₃，…，P_n向x轴作垂线，垂足为Q₁，Q₂，Q₃，…，Q_n，
记梯形P_nP_n+1Q_n+1Q_n的面积为b_n，
则b_n=$\frac{n+n+1}{2}×{2}^{n-1}$=（2n+1）×2^n-2，
∴T_n=3×2^-1+5×2⁰+7×2¹+…+（2n+1）×2^n-2，①
∴2T_n=3×2⁰+5×2¹+7×2²+…+（2n+1）×2^n-1，②
①-②得：-T_n=$\frac{3}{2}$+（2+2²+…+2^n-1）-（2n+1）×2^n-1
=$\frac{3}{2}$+$\frac{2（1-{2}^{n-1}）}{1-2}$-（2n+1）×2^n-1=-$\frac{1}{2}$+（1-2n）×2^n-1．
∴T_n=$\frac{（2n-1）×{2}^{n}+1}{2}$．

点评 本题考查了等比数列的性质，错位相减法求和，属于中档题．